Introducción
Cuantificar el error es un paso importante en la solución aproximada de problemas, pues muchas de las decisiones que se toman en ingeniería se basan en medidas de experimentos y por lo tanto resulta indispensable expresar dichos resultados con claridad y precisión.
En esta unidad se abordan los principales conceptos de la teoría del error, la aproximación a funciones por medio de series y la aproximación a valores de integrales.
Propósitos de aprendizaje
Propósito general
Reconocer tipos de errores inmersos en las aproximaciones numéricas.
Propósitos específicos
- Cuantificar el error y reconocer los tipos de errores.
- Representar funciones y aproximar el valor de ellas usando series de Taylor y de Maclaurin.
- Identificar el método más apropiado para encontrar valores numéricos de integrales complejas.
Error
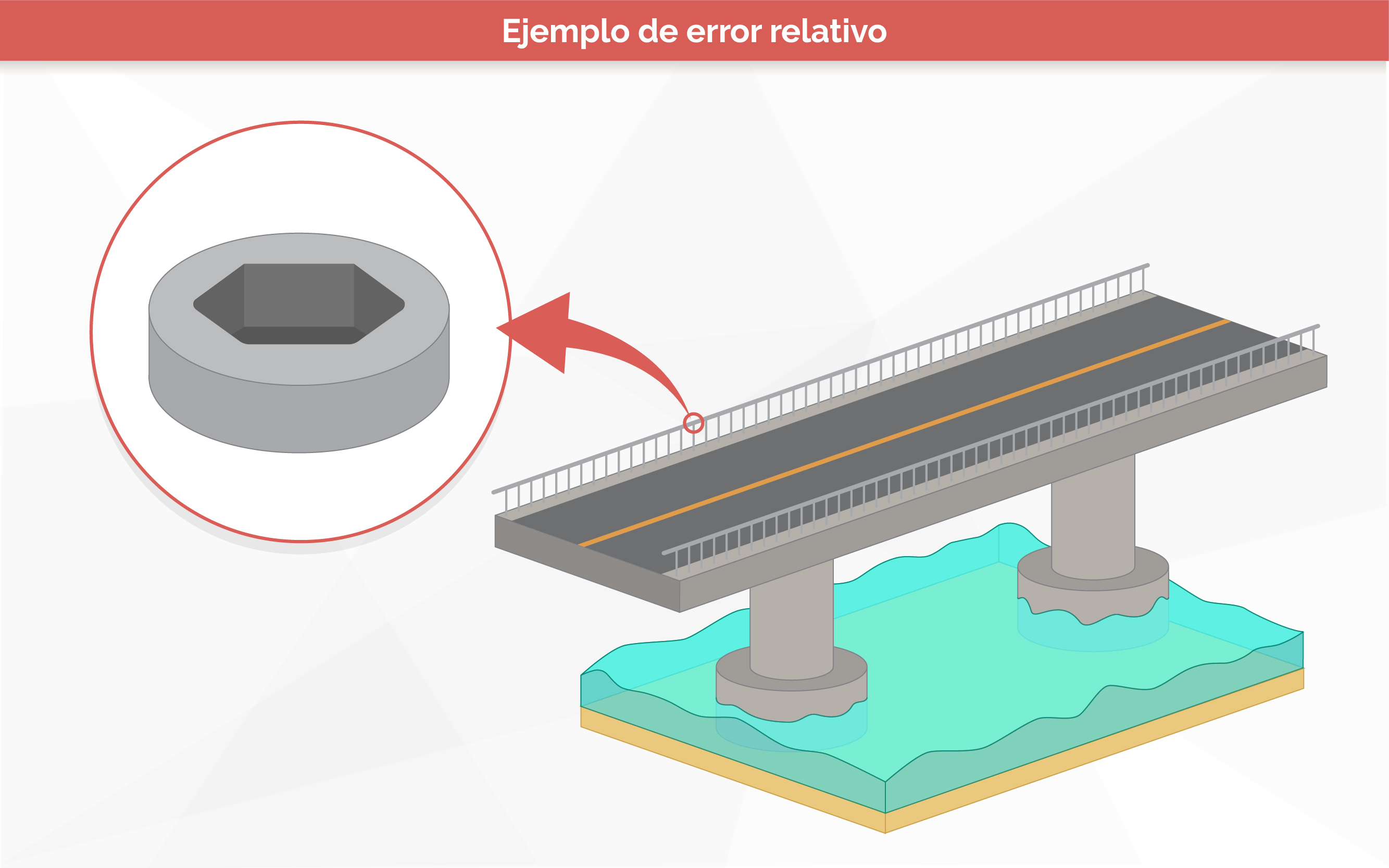
Medir consiste en comparar un objeto físico con otro de la misma naturaleza que es tomado como patrón. Cuando se mide una cantidad, de manera directa o indirecta, esta medición se encuentra sujeta a una incertidumbre que puede originarse por distintas causas.
En esencia nunca se logrará obtener el valor exacto de una magnitud, sino una aproximación a esta, por lo cual se debe indicar lo buena que resulta ser dicha aproximación.
Así las cosas, es necesario que el valor de una medida se acompañe siempre de una posible estimación del error, con el fin de saber que tan fiables son los resultados obtenidos.
 |
Teoría de errores Es el conjunto de reglas dedicadas al estudio de errores y resulta de vital importancia para obtener todo el provecho posible de un conjunto de datos experimentales y evaluar la fiabilidad de estos. |
Error
Errores experimentales
Los errores experimentales son aquellos que provienen de los datos o de equivocaciones aritméticas en el cálculo manual. Ocurren por la presencia de algún factor que no había sido tenido en cuenta y que altera de modo significativo el resultado de la medición.
Ejemplos:
- Errores de calibración en el instrumento de medición.
- No tomar en consideración las fuerzas de rozamiento.
- No esperar a que la aguja de un instrumento como el amperímetro esté en cero antes de efectuar la medición.
Error
Errores de redondeo
Los errores de redondeo ocurren cuando un instrumento de medición numérica, como una calculadora, muestra una cantidad finita de dígitos que no es fiable, pero para saber si una cifra es fiable o no, se debe entender el concepto de cifra significativa. Haga clic sobre el enlace para conocerlo.
Para redondear el error de una medición se suele dar una o dos cifras significativas. Los criterios habituales para darlas son:
- Si la primera cifra que se descarta es cinco o mayor, la última cifra que se guarda se aumenta en una unidad. Es decir que el valor 0.382 se puede redondear como 0.4 y no como 0.3. Si por el contrario, la cifra es menor a cinco se mantiene la unidad anterior, por ejemplo, el valor 0.342 se convierte en 0.3 y no en 0.4.
- Una vez redondeado convenientemente el error, el valor de la medida se redondea hasta la misma cifra decimal.
Existen dos maneras de representar este tipo de errores: por redondeo y por exactitud y precisión. Haga clic sobre el esquema interactivo para ampliar estos dos conceptos.
Error
Errores de truncamiento
Los errores de truncamiento son aquellos que resultan al usar una aproximación en lugar de un procedimiento matemático exacto. Por ejemplo, al calcular la derivada de una velocidad en caída mediante una ecuación en diferencia finita o al calcular el valor de una integral usando métodos de integración numérica.
Error
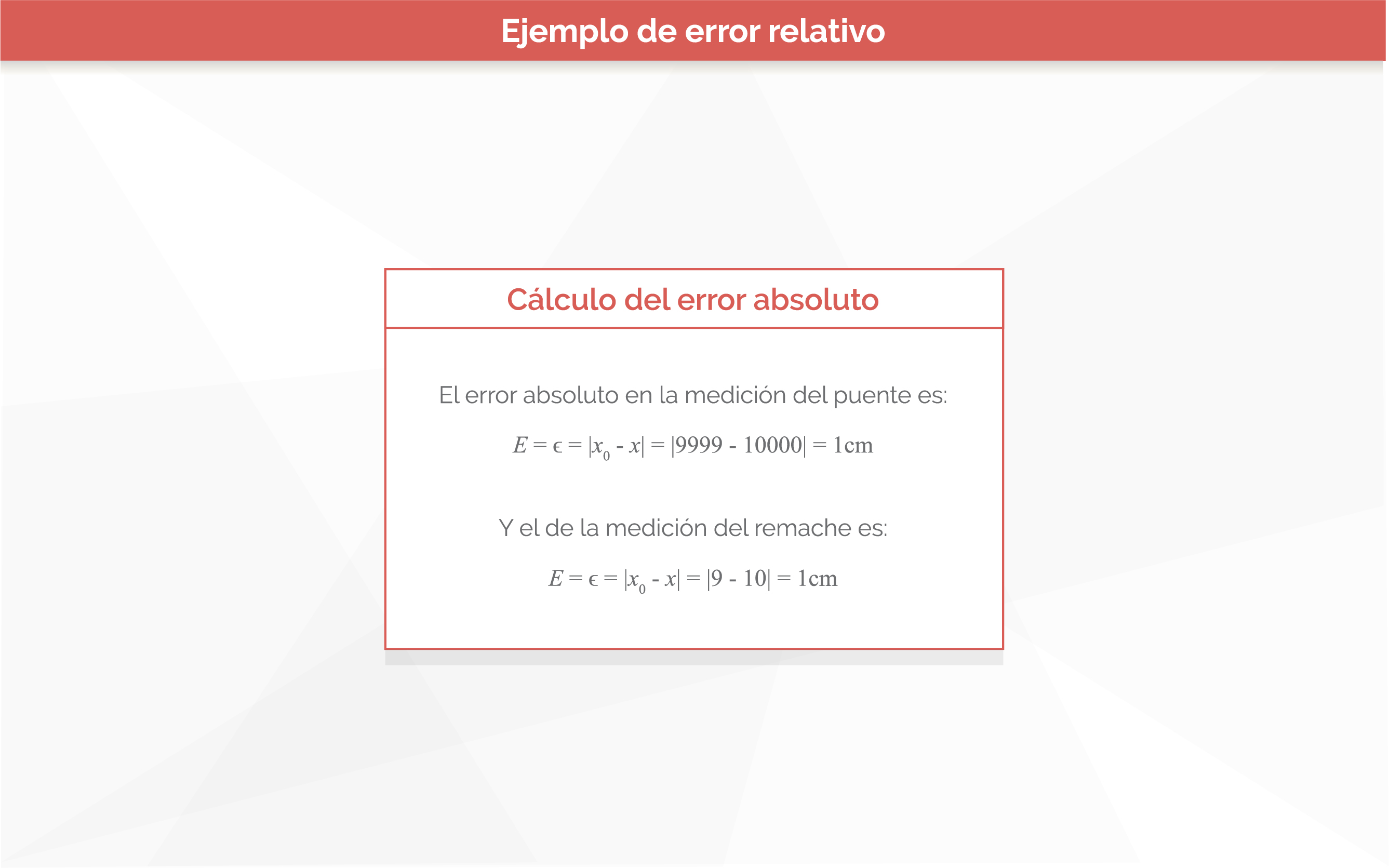
Error absoluto
Si se realiza una medida directa de una cantidad física el valor real x diferirá del valor x0. A esta diferencia se le conoce como error absoluto o simplemente error y se presenta cuando se aproxima el valor real a un valor cercano.
Error
Error relativo
El error relativo es el cociente entre el error absoluto y el valor real, y a partir de este se obtiene el error relativo porcentual.
El error relativo porcentual suele ser un mejor indicador de la precisión debido a que no depende de la escala a utilizar, lo cual es una propiedad supremamente importante.
Error
Error normalizado porcentual
De acuerdo con Chapra y Canale (2007), a veces resulta difícil contar con el valor verdadero en situaciones reales. En estos casos una alternativa es normalizar el error usando la mejor estimación posible al valor verdadero, es decir:
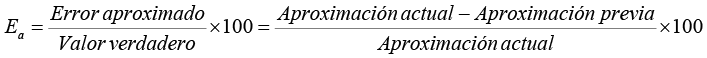
Corrección: λ=x0-x=-ϵ
Valor verdadero: x=x0+λ
Tolerancia
El nivel de tolerancia se define como Es=/0.5X102-n siendo n el número de cifras significativas.
Haga clic sobre este enlace para consultar una aplicación en la que podrá establecer los lados del polígono para ver la forma en que varía la aproximación del cálculo al valor real.
Así mismo, y para concluir este tema, le sugerimos revisar las siguientes actividades de aprendizaje para poner en práctica los conceptos aprendidos, y la ampliación temática para ver un resumen de los errores estudiados.
Actividad de aprendizaje
 |
A continuación le proponemos dos actividades de aprendizaje. En la primera deberá calcular unos determinados errores, mientras que en la segunda deberá hacer un cálculo con tres instrumentos de uso común. Haga clic sobre los enlaces para acceder a las actividades: |
Series
Una serie es la expresión de la suma de cierta cantidad de términos o todos los términos de una sucesión matemática, es decir, es el resultado de realizar la suma:
Siendo cada an un término de una sucesión, así, esta se puede identificar bien sea como una suma parcial:
O como la respectiva suma asociada, que es cuando el valor de n tiende a infinito:
Series
Series de potencia
La serie de Taylor es uno de los objetos de estudio de esta unidad, pero antes de hablar de ella resulta indispensable definir el concepto de series de potencia.
Una serie de potencia es la suma infinita de términos de la forma cnxn en los que x es un valor variable y cn son elementos constantes denominados coeficientes de la serie. Finalmente, la forma de la serie es:
Esta serie, para cada valor de x, se convierte en una serie de coeficientes que permite probar si la serie es convergente o divergente, lo cual significa que puede ser convergente para algunos valores de x y divergente para otros. La suma de la serie resulta ser una función de la forma:
El dominio de esta última función es el conjunto de todos los valores de x para los que la serie resulta ser convergente. Como se puede ver, la forma de f es similar a la de un polinomio, salvo que f tiene una cantidad infinita de términos.
Series
Series de Taylor y Maclaurin
Tras conocer el concepto de series de potencia y entender que las series son funciones, surge una nueva pregunta: ¿qué tipo de funciones se pueden representar por medio de series de potencia?
Comience por suponer que f es una función cualquiera que se puede escribir como una serie de potencias:
Con radio de convergencia: |x-a|<R.
Ahora la pregunta a resolver es: ¿cuál es el valor que debe tomar cada uno de los coeficientes cn? Haga clic sobre el enlace para conocer la respuesta.
Aproximación de series de Taylor y Maclaurin con y sin error
En el esquema interactivo encontrará dos aplicativos diseñados en Geogebra que le permitirán interactuar y decidir qué función trabajar y cuál aproximar. Además, podrá modificar el grado de aproximación a dicha función y ver las gráficas original y de aproximación.
Series
Polinomios de Taylor y Maclaurin
Una pregunta que resulta importante responder es: ¿cuándo una función es igual a la suma de su serie de Taylor? En otras palabras, si f es una función que tiene derivadas de todos los órdenes, ¿cuándo será cierto que la función f es igual a la serie?
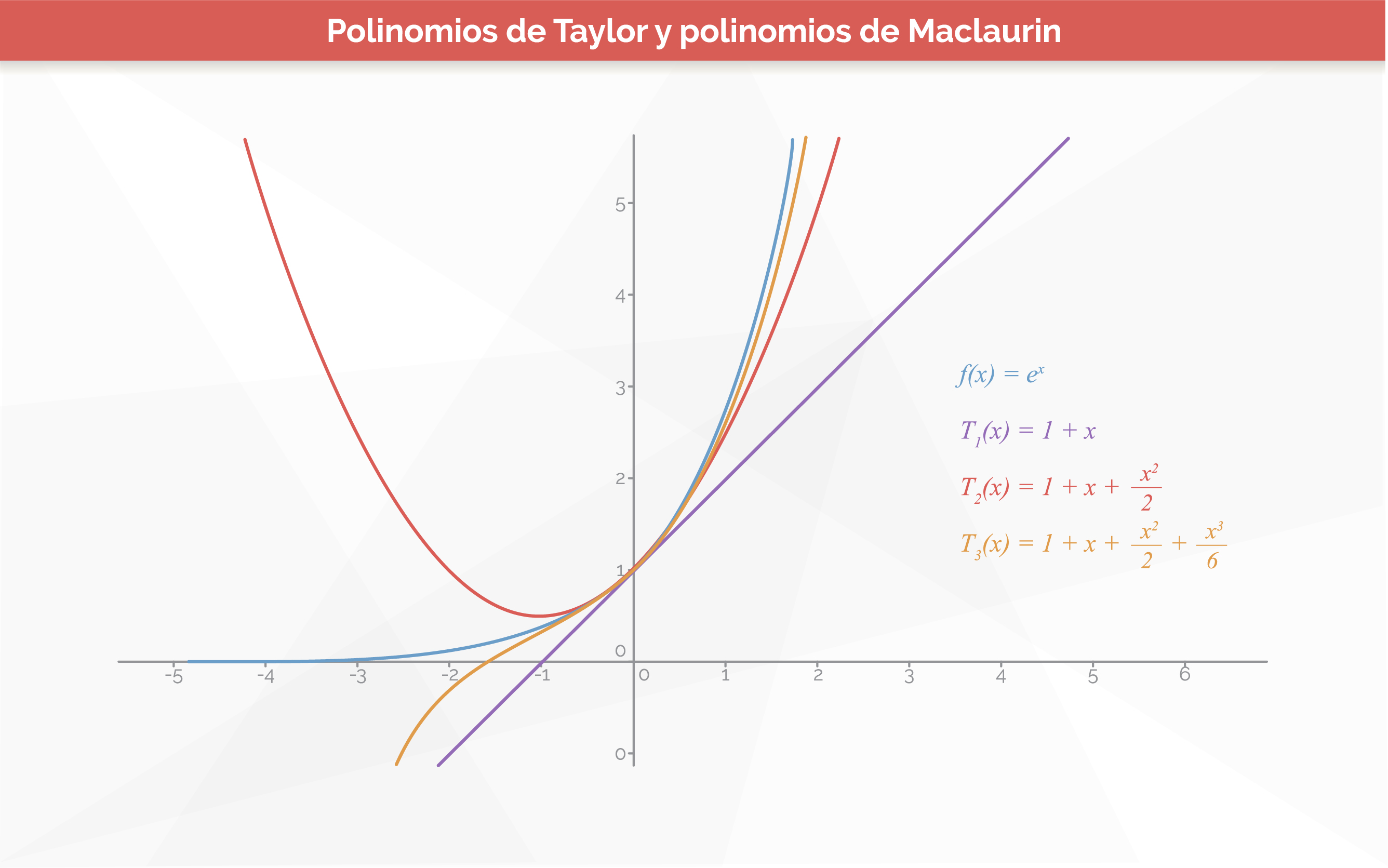
Si f es el límite de la sucesión de sumas parciales para la serie de Taylor, dichas sumas parciales están dadas por:
En este orden de ideas se puede observar que Tn(x) es un polinomio de orden n para toda n, llamado polinomio de Taylor centrado en a. Haga clic sobre la ampliación temática para conocer algunos ejemplos de aplicación de este teorema.
Actividad de aprendizaje
 |
Haga clic sobre el enlace para acceder a una actividad en la que podrá poner a prueba los conocimientos que adquirió sobre aproximación de valores. |
Métodos de integración numérica
Existen algunas integrales definidas de la forma:
Este tipo de integrales no se pueden calcular usando el teorema fundamental del cálculo, pues existen funciones que no tienen una primitiva elemental, es decir que no existen funciones elementales para expresar la integral indefinida de dichas funciones.
Por esta razón se suele recurrir a algunos métodos numéricos que permiten obtener un valor aproximado a este tipo de integrales. Algunos de ellos son los métodos de: el trapecio, el punto medio, Simpson 1/3 y Simpson 3/8.
Métodos de Newton-Cotes
Debido a que resulta imposible calcular algunas integrales definidas existen métodos que en lugar de integrar la función f recurren a integrar un polinomio de interpolación que aproxime a la función f en un intervalo [a, b].
Estos son conocidos como los métodos de Newton-Cotes y constituyen una familia general de métodos que se dividen según el polinomio mediante el cual se desee trabajar, según el grado, según diferentes puntos para interpolar, etc. A continuación se trabajarán polinomios de interpolación de grado 1 y 2 asociados respectivamente a los métodos: del trapecio y Simpson.
Métodos de integración numérica
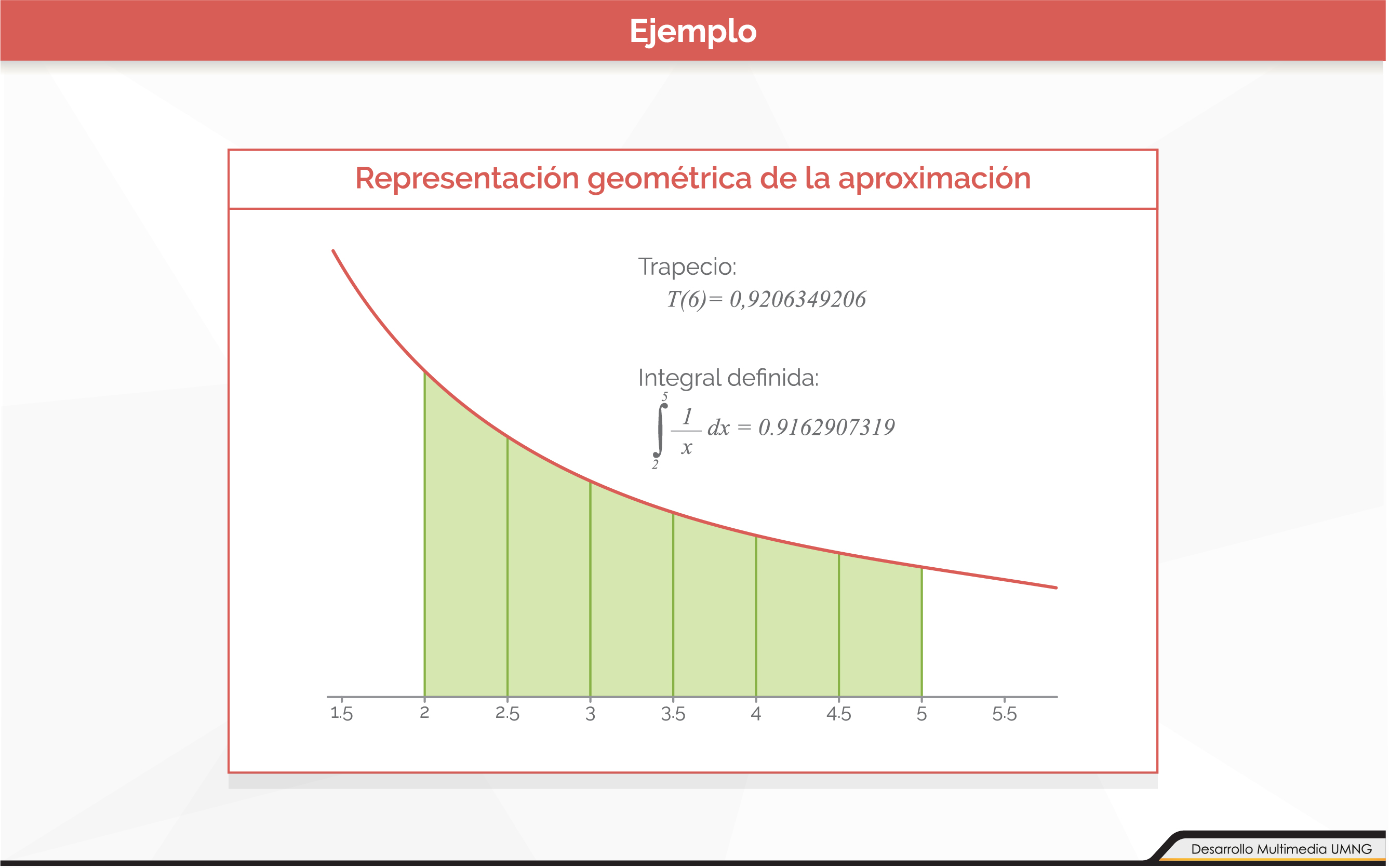
Método del trapecio
El método del trapecio es un método de Newton-Cotes basado en interpolación lineal, cuya idea para aproximar el valor de la integral de f(x) en un intervalo [a, b] es aproximar a f por medio de su polinomio de interpolación Pn(x) en dicho intervalo. Este polinomio interpolante se puede calcular usando la forma de Lagrange para Pn(x), siendo n≥1 la cantidad de subintervalos. Entonces:
Siendo:
Haga clic aquí para ampliar esta explicación.
Método del trapecio compuesto
Si el intervalo en el que se quiere calcular la integral es bastante grande, el método descrito anteriormente resulta ineficaz e impreciso. Por esta razón, y para mejorar la exactitud, es posible subdividir el intervalo en otros más pequeños aplicando en cada uno de ellos el método del trapecio simple. Haga clic sobre el enlace para profundizar en este concepto.
Métodos de integración numérica
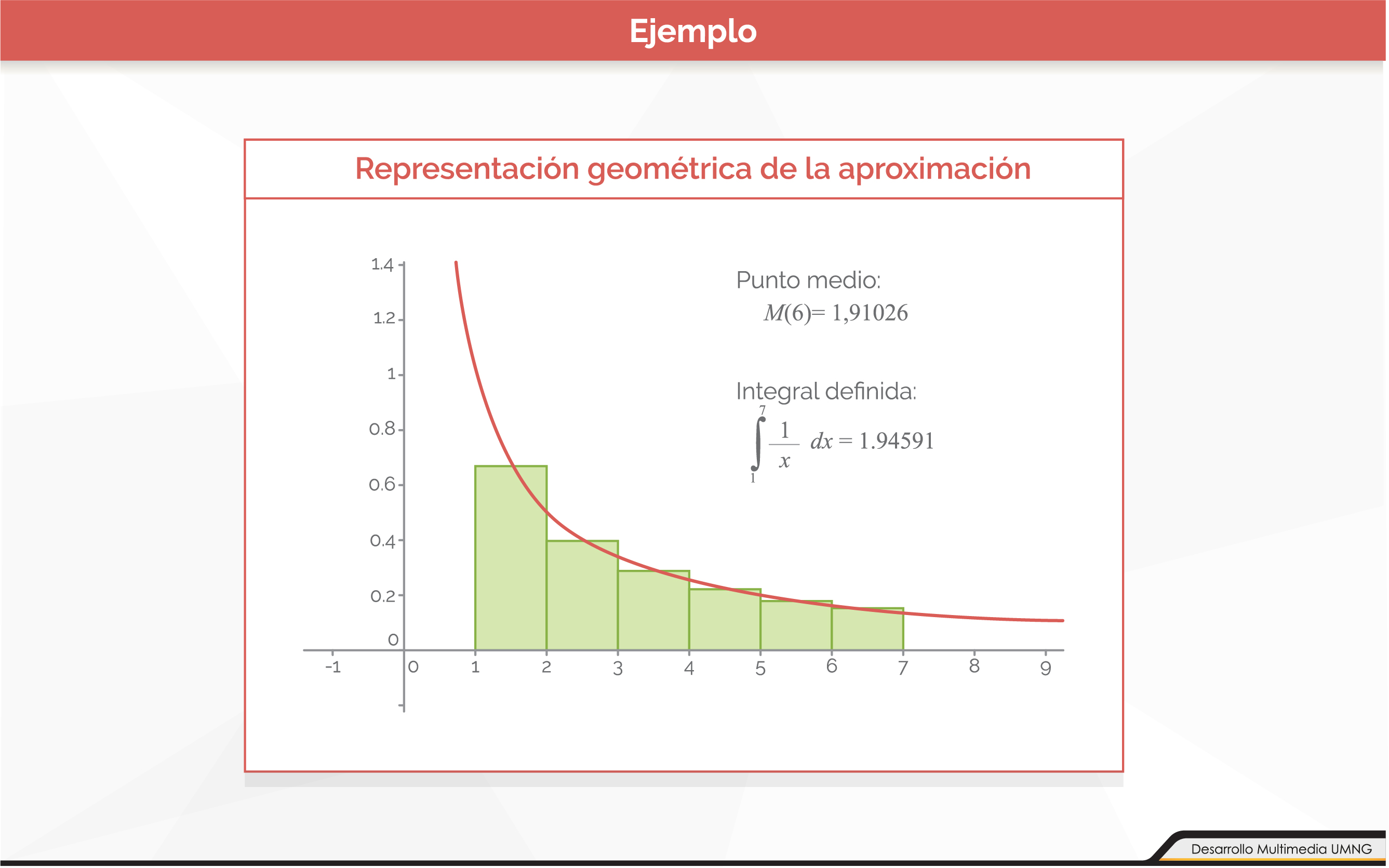
Método del punto medio
El método del punto medio es otro de los método de Newton-Cotes que consiste en aproximar el valor real de una integral en un intervalo [a, b] por medio de rectángulos de base (b-a) y altura f(b+a/2). Es por esta razón que el método recibe el nombre de «punto medio».
Haga clic sobre el enlace para ver la forma en que se aplica el método del punto medio.
Métodos de integración numérica
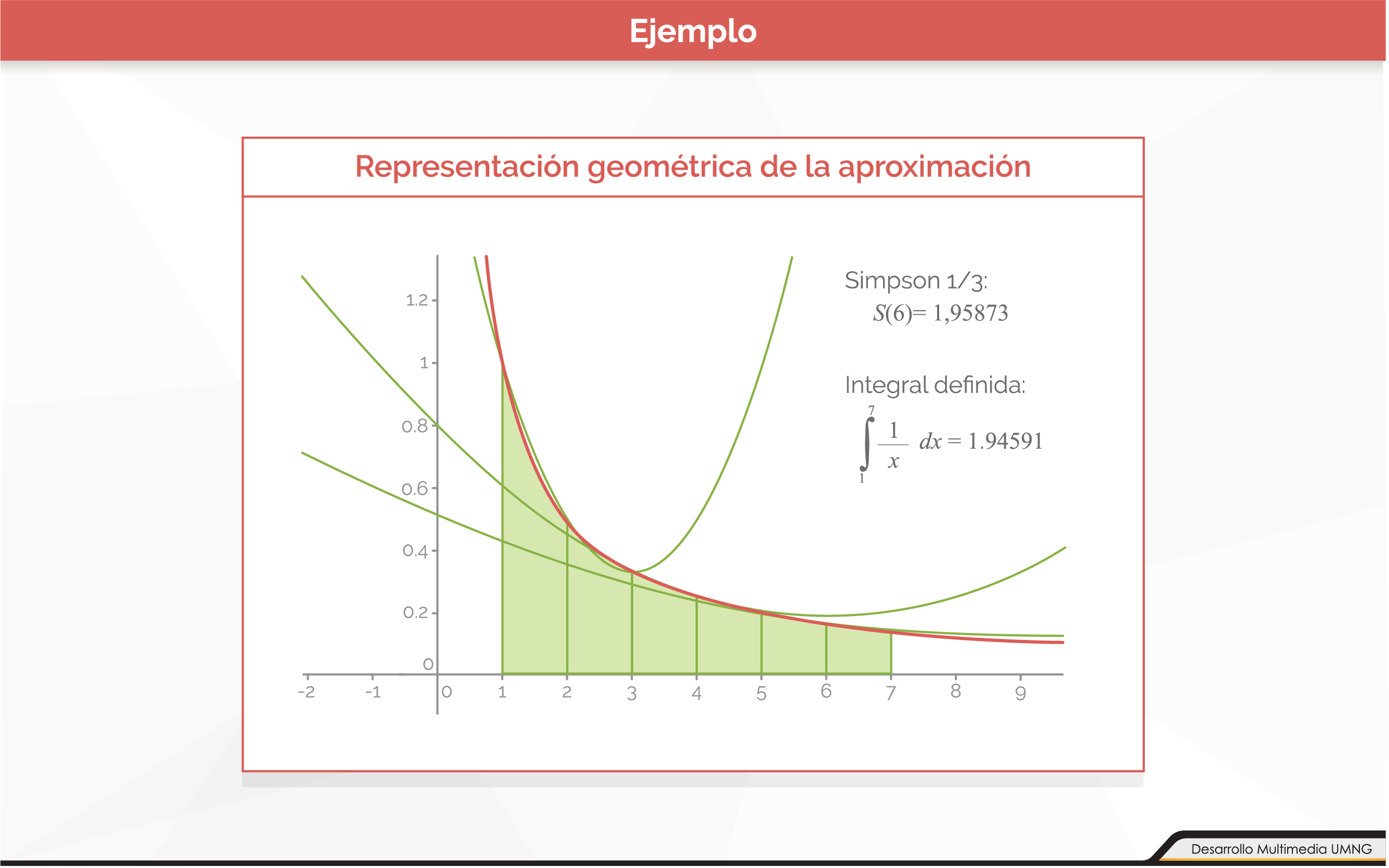
Método de Simpson 1/3
El método de Simpson es otro de los método de Newton-Cotes que consiste en integrar un polinomio de interpolación. Cuando el polinomio es de grado dos se denomina método 1/3 y cuando el polinomio es de grado tres se llama método 3/8.
En el caso del método 1/3, si se tiene una función f(x) en el intervalo [a, b] se debe tomar como el tercer punto de interpolación al punto medio del intervalo, que se llama:
Mientras que a la semianchura del intervalo se denomina:
Haga clic sobre el enlace para ver la forma en que se aplica el método de Simpson 1/3.
Métodos de integración numérica
Método de Simpson 3/8
Al igual que con el método de Simpson 1/3, con este método podemos realizar una aproximación, pero esta vez por medio de un polinomio de interpolación de tercer grado P3(x), partiendo del intervalo [a, b] en tres subintervalos e integrando:
Para así, obtener la expresión de aproximación a la integral inicial:
Donde:
Representa la anchura de los subintervalos. Haga clic sobre el enlace para ampliar esta explicación.
 |
A manera de repaso le sugerimos revisar la ampliación temática en la que encontrará de forma resumida todas las formulas presentadas para los diferentes métodos de integración numérica. |
Para finalizar, revise el aplicativo que aparece en pantalla, en el que podrá decidir qué función es la que desea integrar, el intervalo de integración y cuántos subintervalos desea para ello, así como cuál es el método que prefiere usar para esto (trapecio, Simpson o punto medio).
Actividad de aprendizaje
 |
Haga clic sobre el enlace para acceder a una actividad que le permitirá poner en práctica los métodos de integración estudiados. |
Resumen
En esta unidad se ofreció un acercamiento a la noción de error, trabajada desde diferentes perspectivas. Inicialmente se brindó una explicación teórica del error y los tipos de errores que existen, entre los cuales se trabajaron y ejemplificaron el error absoluto, el error relativo y el error relativo porcentual.
Se expusieron y trabajaron las series de Taylor y de Maclaurin, y las aproximaciones a valores de funciones por medio de ellas, lo cual da cabida a la obtención de un error en los cálculos. De esta forma se articularon los dos primeros temas expuestos.
En la segunda parte de la unidad se le ofrecieron herramientas al estudiante para aprender a calcular series de Taylor y de Maclaurin, y polinomios asociados a estas series. Estas herramientas le permitirán al estudiante encontrar las gráficas aproximadas de las funciones, al menos en cierto intervalo.
Para finalizar, se expusieron algunos métodos de integración numérica denominados métodos Newton-Cotes, que se refieren a la aproximación de integrales por medio de la integración de polinomios de interpolación de Lagrange. En esta sección se trabajó con polinomios de interpolación de grado 0, 1, 2 y 3, dando origen a los métodos del punto medio, del trapecio, de Simpson 1/3 y de Simpson 3/8.
Bibliografía ()
- Chapra, S., y Canale, R. (2007). Métodos numéricos para ingenieros. 5. ª ed. México. Interamericana Editores.
- Hurtado, A., y Domínguez, F. (2014). Métodos numéricos aplicados a ingeniería. México: Grupo Editorial Patria.
- Jiménez, V., y Pallarés, A. (2008). Métodos numéricos. Universidad de Murcia: Uruguay.
- Lagos, J. (2017). Sucesiones numéricas. [Ilustración].
- Mora, W. (2016). Introducción a los métodos numéricos. Costa Rica: Instituto Tecnológico de Costa Rica.
Referencias Web
- Maza Gómez, C. (1998). Aproximaciones históricas al área del círculo. Suma (27). pp. 49-56. Recuperado de: https://revistasuma.es/IMG/pdf/27/SUMA_27.pdf.
- Kneller, G. (1689). Portrait of Isaac Newton. [Óleo sobre lienzo]. Recuperado de:https://commons.wikimedia.org/wiki/File:Sir_Isaac_Newton_(1643-1727).jpg.
- S. n. (S. f.). Portrait of Roger Cotes. [Escultura]. Recuperado de: https://commons.wikimedia.org/wiki/File:Roger_Cotes.png.