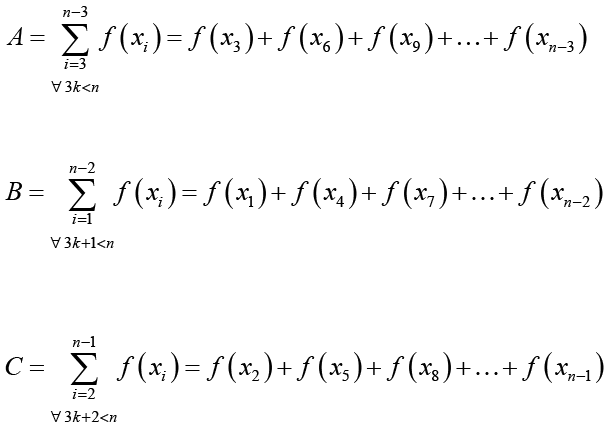Fórmulas de los diferentes métodos de integración numérica
(Resumen)

Polinomio interpolante de Lagrange:

{{P}_{n}}\left( x \right)={{L}_{n,0}}\left( x \right)f\left( {{a}_{0}} \right)+{{L}_{n,1}}\left( x \right)f\left( {{a}_{1}} \right)+{{L}_{n,2}}\left( x \right)f\left( {{a}_{2}} \right)+\ldots {{L}_{n,n}}\left( x \right)f\left( {{a}_{n}} \right)

Siendo:

{{L}_{n,k}}\left( x \right)=\underset{\begin{matrix} i=0 \\ i\ne k \\ \end{matrix}}{\overset{n}{\mathop \prod }}\,\frac{x-{{x}_{i}}}{{{x}_{k}}-{{x}_{i}}}

Método simple del trapecio:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \underset{a}{\overset{b}{\mathop \int }}\,{{P}_{1}}\left( x \right)dx=\frac{b-a}{2}\left( f\left( a \right)+f\left( b \right) \right)

Método compuesto del trapecio:

I\approx \underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{h}{2}\left( f\left( {{x}_{0}} \right)+2\underset{i=1}{\overset{n-1}{\mathop \sum }}\,f\left( {{x}_{i}} \right)+f\left( {{x}_{n}} \right) \right)

Siendo:

h=\frac{b-a}{n}

Método del punto medio:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \left( b-a \right)f\left( \frac{b+a}{2} \right)

Método compuesto del punto medio:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx h\left( \underset{i=1}{\overset{n}{\mathop \sum }}\,f\left( \frac{{{x}_{i}}+{{x}_{i-1}}}{2} \right) \right)

Siendo:

h=\frac{b-a}{n}

Método de Simpson 1/3:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \underset{a}{\overset{b}{\mathop \int }}\,{{P}_{2}}\left( x \right)dx=\frac{h}{3}\left( f\left( a \right)+4f\left( {{x}_{m}} \right)+f\left( b \right) \right)

Método de Simpson 1/3 compuesto:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{h}{3}\left( f\left( a \right)+4I+2P+f\left( b \right) \right)

Siendo:

I=\underset{i=1,~impares}{\overset{n-1}{\mathop \sum }}\,f\left( {{x}_{i}} \right)=f\left( {{x}_{1}} \right)+f\left( {{x}_{3}} \right)+f\left( {{x}_{5}} \right)+\ldots +f\left( {{x}_{n-1}} \right)

P=\underset{i=2,~pares}{\overset{n-2}{\mathop \sum }}\,f\left( {{x}_{i}} \right)=f\left( {{x}_{2}} \right)+f\left( {{x}_{4}} \right)+f\left( {{x}_{6}} \right)+\ldots +f\left( {{x}_{n-2}} \right)

Método de Simpson 3/8:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \left( b-a \right)\frac{f\left( {{x}_{0}} \right)+3f\left( {{x}_{1}} \right)+3f\left( {{x}_{2}} \right)+f\left( {{x}_{3}} \right)}{8}

Método de Simpson 3/8 compuesto:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{3h}{8}\left( f\left( a \right)+2A+3B+3C+f\left( b \right) \right)

Siendo: