Introducción
Las distribuciones de probabilidad son los posibles valores que resultan de un experimento aleatorio, junto con la probabilidad asociada a cada valor y la distribución de frecuencias. Facilita el manejo de cantidades de información en forma resumida, al describir un hecho anterior, pasado o transcurrido (en contraste con la distribución de probabilidades, que presenta valores probables de un experimento en un evento futuro).
Las variables aleatorias hacen referencia a la caracterización cualitativa de los resultados, que constituyen un espacio muestral. Cada cantidad o valor es el resultado de un experimento aleatorio y puede tomar distintos valores (se clasifican en discretas y continuas). Las discretas son valores que se pueden contar y organizar en una secuencia (como los enteros positivos) y sólo asumen valores finitos.
Las variables aleatorias continuas hacen referencia a valores dentro de un intervalo o en la unión de varios intervalos. Admiten funciones y valores decimales; además consideran el modelo normal estandarizado.
Objetivos
Objetivo general
Aplicar el uso de la probabilidad en la toma de decisiones, diferenciando las distintas distribuciones de probabilidad en la solución de problemas contextualizados a su carrera.
Objetivos específicos
-
Explicar y diferenciar una distribución probabilística y una distribución de frecuencias.
-
Definir e identificar una variable aleatoria discreta y una continua.
- Identificar las condiciones que deben existir para el uso de cada una de las distribuciones: binomial, de Poisson, geométrica y normal, entre otras.
- Construir, aplicar y calcular probabilidades asociadas a estas distribuciones.
Distribución de probabilidad (conceptos básicos)
En las variables aleatorias los valores dependen del resultado de un proceso aleatorio (llamado variable aleatoria). Se denotan con letras mayúsculas (X, Y, Z) y sus valores correspondientes, con minúsculas, donde X=x. Las hay de dos tipos:
La función de probabilidad aleatoria o distribución de probabilidad es 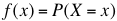 . Es la probabilidad de que X asuma el valor de x (Ver características de Distribución de probabilidad discreta y probabilidad continua). El valor esperado de que ocurra un suceso será o esperanza de X o media de X. Se denota de la siguiente manera:
. Es la probabilidad de que X asuma el valor de x (Ver características de Distribución de probabilidad discreta y probabilidad continua). El valor esperado de que ocurra un suceso será o esperanza de X o media de X. Se denota de la siguiente manera:
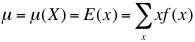
También será necesario para hallar con mayor precisión los valores esperados, la varianza y la desviación estándar de la variable:
-
Varianza:
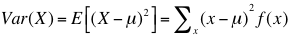
-
Desviación estándar de la variable:
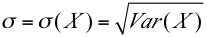
Distribuciones discretas
Las distribuciones discretas, como anteriormente se ha mencionando, son valores que se pueden contar y organizar en una secuencia (como los enteros positivos) y sólo asumen valores finitos.
Dentro de los modelos de probabilidad correspondiente a variables aleatorias discretas, con mayor aplicación están:
- Bernoulli
- Binomial
- Poisson
- Exponencial
- Geométrica
Distribuciones discretas
Distribución binomial
El modelo de la distribución binomial posee las siguientes características:
- En cada prueba del experimento sólo son posibles dos resultados: el suceso A (éxito) y su contrario (fracaso).
- El resultado obtenido en cada prueba es independiente de los resultados obtenidos anteriormente.
- La probabilidad del suceso A es constante, la representamos por p, y no varía de una prueba a otra. La probabilidad es 1- p y la representamos por q.
- El experimento consta de un número n de pruebas.
La variable aleatoria binomial (variable X) expresa el número de éxitos obtenidos en cada prueba del experimento. La variable binomial es del tipo aleatoria discreta (sólo puede tomar los valores 0, 1, 2, 3, 4,n.) si se han realizado n pruebas. Como hay que considerar todas las maneras posibles de obtener k-éxitos y (n-k) fracasos, debemos calcularlas por combinaciones (número combinatorio n sobre k).
La distribución binomial se suele representar por B (n,p) siendo n y p los parámetros de dicha distribución (ver función de distribución binomial). La función de probabilidad de la distribución binomial también es denominada función de la distribución de Bernoulli (para n=1).
Si X es el número de éxitos en n ensayos independientes de un experimento binomial con probabilidad p de éxito y q de fracaso en cualquier ensayo, entonces la distribución f está dada por:
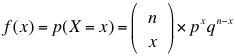
Donde el factor 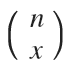 es una permutación que se resuelve:
es una permutación que se resuelve:
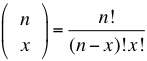
Distribuciones discretas
Distribución de Poisson
Esta distribución es una de las más importantes en la variable discreta. Sus principales aplicaciones están relacionadas con la modelización de situaciones para determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas. Hace referencia a procesos descritos con variables aleatorias discretas. La letra x representa esa variable y asume valores enteros (0, 1, 2,3 etc...). X (mayúscula) representa la variable aleatoria y la x (minúscula) designa un valor específico que asume la X mayúscula. La probabilidad de exactamente x ocurrencias en una distribución de Poisson se calcula por la siguiente fórmula:
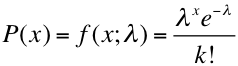
Donde Lambda es el número medio o promedio de eventos por intervalo de tiempo elevada al exponente x. Otro de sus usos es la consideración límite de procesos dicotómicos, reiterados un gran número de veces si la probabilidad de obtener un éxito es muy pequeña. Esta distribución se puede derivar de un proceso experimental de observación.
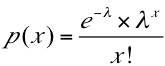
Donde 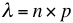 es decir, el número de veces n que se realiza un experimento multiplicado por la probabilidad p de éxito en cada ensayo. X es el número de éxito cuya probabilidad se está calculando. En consecuencia, en un intervalo infinitésimo podrán producirse O ó 1 hecho, pero nunca más de uno. Se define como el número de hechos que ocurren en un intervalo unitario de tiempo o espacio. La función de distribución está dada por la siguiente expresión:
es decir, el número de veces n que se realiza un experimento multiplicado por la probabilidad p de éxito en cada ensayo. X es el número de éxito cuya probabilidad se está calculando. En consecuencia, en un intervalo infinitésimo podrán producirse O ó 1 hecho, pero nunca más de uno. Se define como el número de hechos que ocurren en un intervalo unitario de tiempo o espacio. La función de distribución está dada por la siguiente expresión:
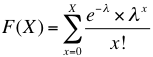
Distribuciones discretas
Distribución geométrica
La distribución geométrica o de Pascal es un modelo adecuado para aquellos procesos en los que se repiten pruebas hasta lograr la consecución del éxito al resultado deseado. Implica la existencia de una dicotomía de posibles resultados y la independencia de las pruebas entre sí.
Esta distribución se puede hacer derivar de un proceso experimental puro o de Bernoulli, de acuerdo con las siguientes características:
- El proceso posee un número no definido de pruebas o experimentos separados o separables. Concluirá cuando se obtenga por primera vez el resultado deseado (éxito).
- Cada prueba puede dar dos resultados mutuamente excluyentes: A y no A.
- La probabilidad de obtener un resultado A en cada prueba es p; la de un resultado no A, es q: (p + q = 1).
Las probabilidades p y q son constantes en todas las prueba; por tanto, las pruebas son independientes (si se trata de un proceso de "extracción" se llevará a cabo con devolución del individuo extraído).
Derivación de la distribución
Si las circunstancias permiten una aleatoriedad de forma que tomen como variable aleatoria X = número de pruebas necesarias para obtener por primera vez un éxito o resultado A, esta variable será distribuida con una distribución geométrica de parámetro p. Se halla la función de probabilidad por la siguiente fórmula:
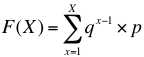
Distribuciones discretas
Distribución binomial negativa
En la distribución de probabilidad de una variable aleatoria binomial negativa (también conocida como distribución de Pascal o de Polya), el número de experimentos de Bernoulli de parámetro 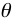 independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y
independientes realizados hasta la consecución del k-ésimo éxito es una variable aleatoria que tiene una distribución binomial negativa con parámetros k y 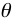 .
.
La distribución geométrica es el caso concreto de la binomial negativa cuando k = 1. Está definida por la siguiente fórmula.
Distribución continua
Una distribución de probabilidad continua se caracteriza porque su función es continua. Puesto que la función de distribución de una variable aleatoria X viene dada por 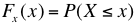 , la definición implica que en una distribución de probabilidad continua X se cumple
, la definición implica que en una distribución de probabilidad continua X se cumple 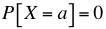 para todo número real a. Esto es la probabilidad que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
para todo número real a. Esto es la probabilidad que X tome el valor a es cero para cualquier valor de a. Si la distribución de X es continua, se llama a X variable aleatoria continua.
En las distribuciones de probabilidad continuas, la distribución de probabilidad es la integral de la función de densidad, por lo que tenemos entonces que:
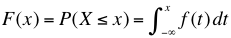
Mientras que en una distribución de probabilidad discreta un suceso con probabilidad cero es imposible, no se da el caso en una variable aleatoria continua (ver ejemplo).
En estas funciones existe el término densidad de probabilidad. Para una variable continua hay infinitos valores posibles de la variable y entre cada dos de ellos se pueden definir infinitos valores más. En estas condiciones no es posible deducir la probabilidad de un valor puntual de la variable (como se puede hacer en el caso de variables discretas), pero es posible calcular la probabilidad acumulada hasta un cierto valor (función de distribución de probabilidad). Es posible analizar cómo cambia la probabilidad acumulada en cada punto (estos cambios no son probabilidades, sino otro concepto: función de densidad).
Distribución continua
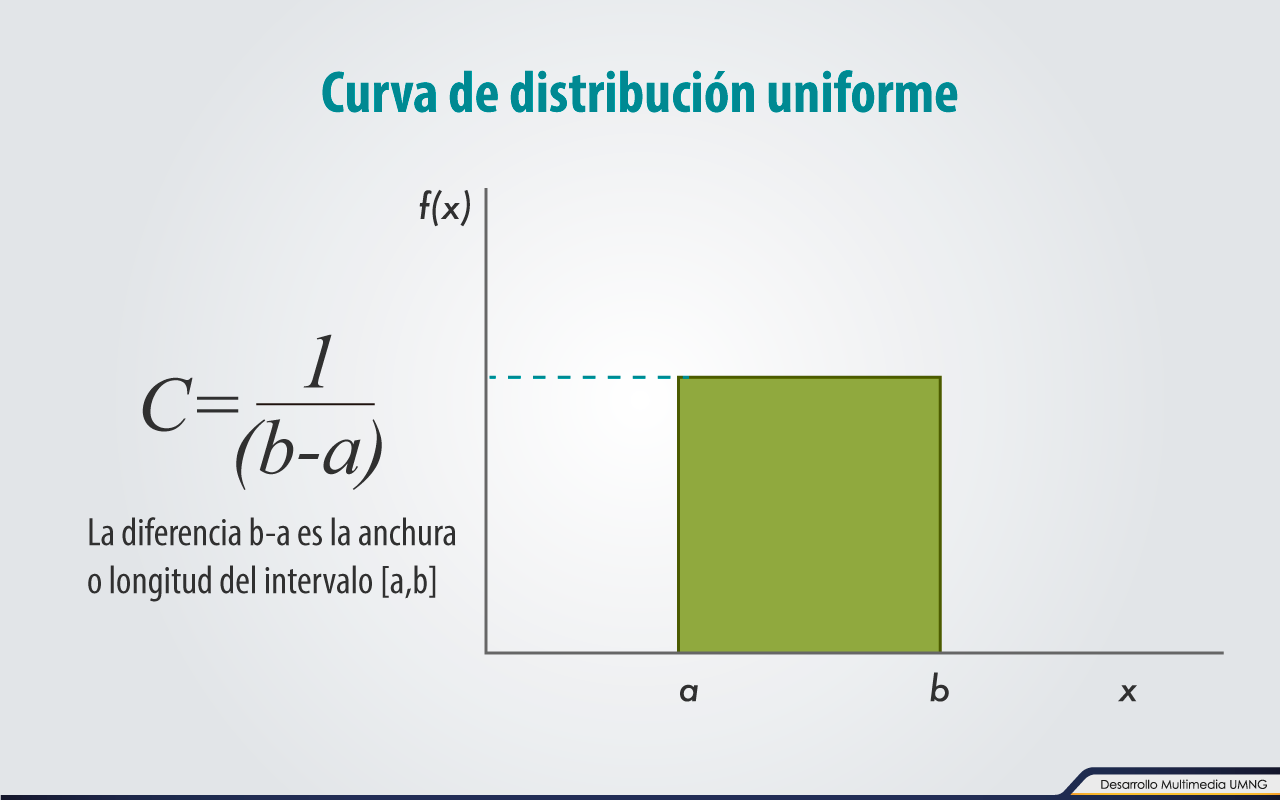
Distribución uniforme
La distribución uniforme es el modelo continuo más simple. Es un ejemplo de una distribución de probabilidad continua en la que los resultados posibles del experimento son obtenidos de variables aleatorias continuas; es decir, de variables cuantitativas que pueden tomar cualquier valor, que resultan principalmente del proceso de medición.
Es una función distribución de probabilidad f(x) que toma un valor constante 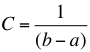 para todo valor de x que se encuentra dentro del intervalo [a,b] y cero en otra parte, luego:
para todo valor de x que se encuentra dentro del intervalo [a,b] y cero en otra parte, luego:
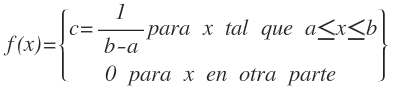
A continuación se presenta un ejemplo de la distribución continua uniforme.
Distribución continua
Distribución exponencial
A pesar de la sencillez analítica de sus funciones de definición, la distribución exponencial tiene gran utilidad práctica. De hecho, la distribución exponencial puede derivarse de un proceso experimental de Poisson con las mismas características de la distribución de Poisson, pero toma como variable aleatoria el tiempo que tarda en producirse un hecho (ver función de densidad).
Obviamente la variable aleatoria será continua. Existe una relación entre el parámetro a de la distribución exponencial y el parámetro de intensidad del proceso l; esta relación es: a = l. Al ser un modelo adecuado para estas situaciones, es de gran utilidad en los siguientes casos:
- Distribución del tiempo de espera entre sucesos de un proceso de Poisson.
- Distribución del tiempo que transcurre hasta que se produce un fallo. Si se cumple la condición que la probabilidad de producirse un fallo en un instante, no depende del tiempo transcurrido.
- Aplicaciones en fiabilidad y teoría de la supervivencia.
La distribución exponencial no tiene memoria: si el elemento a consideración ha sobrevivido un tiempo S (hasta el momento), no modifica la probabilidad de que sobreviva t unidades de tiempo más. La probabilidad que el elemento falle en una hora (un día o un segundo) no depende del tiempo que lleve funcionando. No existe envejecimiento, ni mayor probabilidad de fallos al principio del funcionamiento:
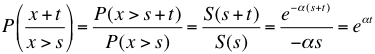
Esta expresión no depende, como se observa, del tiempo sobrevivido s.
Distribución continua
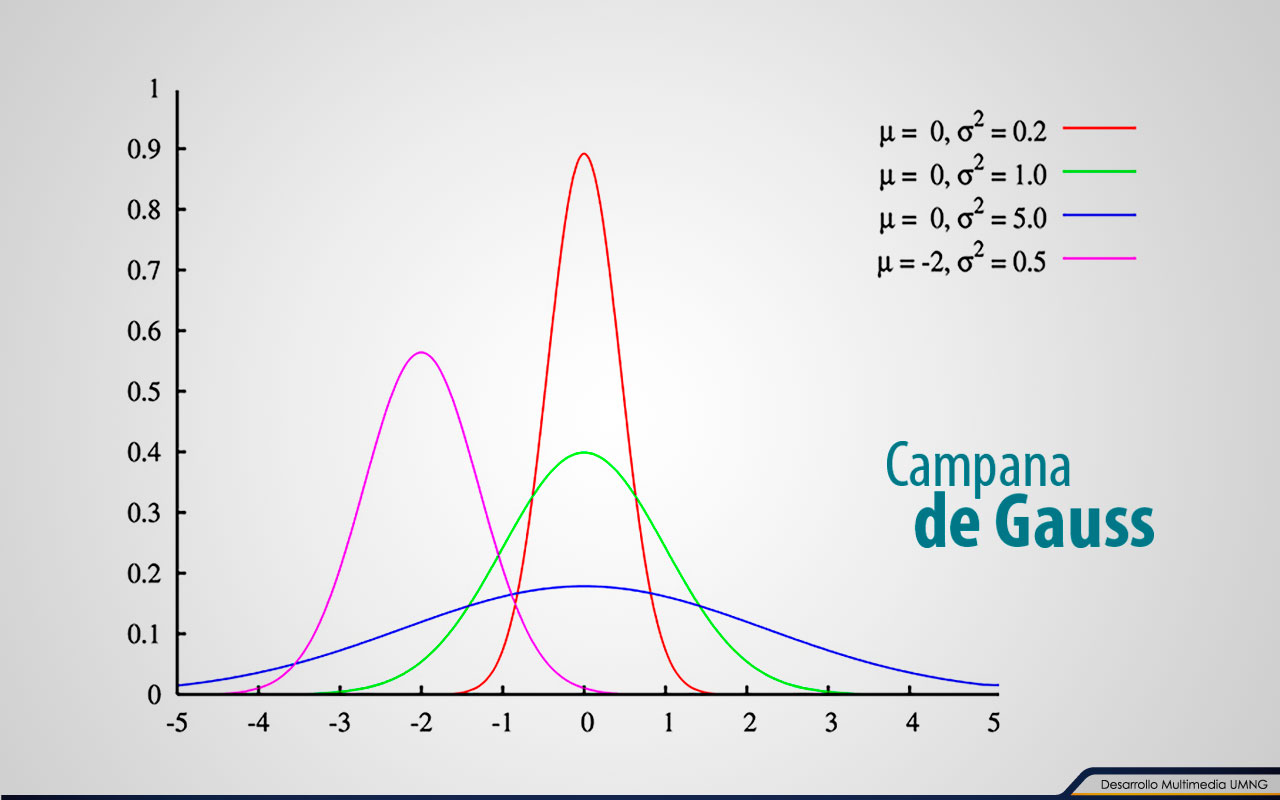
Distribución normal o Gaussiana
La distribución normal es de suma importancia en estadística por tres razones principales:
- Numerosas variables continuas de fenómenos aleatorios tienden a comportarse probabilísticamente mediante ésta.
- Es el límite en el que convergen tanto variables aleatorias continuas como discretas.
- Proporciona la base de la inferencia estadística clásica, debido a su relación con el teorema del límite central.
Las propiedades de la distribución normal son tres. La primera es que su gráfica tiene forma acampanada (campana de Gauss); la segunda, el valor esperado, la mediana y la moda tienen el mismo valor cuando la variable aleatoria se distribuye normalmente; y la tercera, su dispersión media es igual a 1.33 desviaciones estándar. Es decir, el alcance intercuartil está contenido en un intervalo de dos tercios de una desviación estándar debajo de la media, a dos tercios de una desviación estándar sobre la media. Algunas de las variables estudiadas sólo pueden aproximar estas propiedades. Así que, si el fenómeno puede mediarse aproximadamente mediante la distribución normal, resultará que:
- El polígono puede verse en forma de campana y simétrico.
- Sus mediciones de tendencia central tienen bastante parecido.
- El valor intercuartil puede diferir ligeramente de 1.33 desviaciones estándar.
- El dominio de la variable aleatoria normalmente distribuida generalmente caerá dentro de tres desviaciones estándar por encima y por debajo de la media.
Se caracteriza por tener las propiedades de la media y de la varianza.
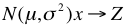
Las variables continuas se estandarizan en una variable Z para poder utilizar la tabla y encontrar las propiedades, teniendo en cuenta los intervalos pedidos y restando la intersección de estos.
Resumen
Toda distribución de probabilidad es generada por una variable aleatoria x, la que puede ser de dos tipos:
La distribución binomial, Poisson y normal se aplican en aquellos experimentos que solo tienen dos resultados: éxitos o fracasos.
La distribución hipergeométrica se aplica al muestrear sin reposición; por tanto, la probabilidad de éxito no es constante. Su cálculo es tedioso cuando n es grande. En muchos casos sus resultados son casi iguales al de la Binomial, por lo que se procede a resolverlos por este último método. Las pruebas son dependientes.
La distribución de Poisson se aplica en ejercicios de Binomial sólo cuando n es muy grande y la probabilidad de éxito es muy pequeña.
En la distribución binomial la probabilidad de éxito debe ser constante para cada ensayo sucesivo.
La distribución normal queda totalmente especificada por su media y desviación estándar; por lo tanto, tendrá una distribución normal diferente para cada media y su desviación estándar.
Bibliografía ()
- Canavos, G. (1987) Probabilidad y estadística: aplicaciones y métodos. México. Editorial Mc Graw Hill.
- Levin, R; Rubin, D. (2010) Estadísticas para administración y economía. México. Editorial Pearson - Prentice Hall.
- Martínez, C. (2012) Estadística y muestreo. 13ª edición. Bogotá: Editorial ECOE.
- Mason, R; Lind, D. (2004) Estadística para administración y economía. 11ª edición. Bogotá. Editorial Alfa Omega.
- Mendenhall, W. (1990) Estadística para administradores. 2ª edición. México. Grupo editorial Iberoamérica.
- Milton, J; Jesse C. (2004) Probabilidad y estadística. 4ª edición. México. Editorial Mc Graw Hill
- Walpole, R; Meyers, R (2004) Probabilidad y estadística para ingenieros. 8ª edición. México. Editorial Prentice Hall.