Introducción
Esta unidad abarca el concepto de probabilidad (así como su manejo y dominio) a partir del cálculo de problemas reales y cotidianos, debido a que es una de las más complejas ramas de las matemáticas, razón por la que veremos cómo y de qué manera son resueltos algunos problemas mediante los cálculos probabilísticos.
Es importante conocer las claves que conllevan a hablar de probabilidad, como las técnicas de conteo (que no son material exclusivo de la probabilidad, sino una pequeña parte de las matemáticas, muy utilizadas en la cotidianidad), junto con otros conceptos relacionados para comprender el objeto de estudio de la probabilidad, tales como los cálculos de probabilidad y los métodos probabilísticos, fundamentales para determinar el análisis de la función de probabilidad y sus diversas distribuciones.
Esta unidad mostrará aplicaciones directas, como la incidencia en la toma de decisiones sobre la aceptación de un riesgo, estructurando variables que identifican la posibilidad de ocurrencia de un suceso que desestabilice las condiciones normales de la prestación de un servicio o la utilización de un bien.
La probabilidad en la toma de decisiones también cumple un papel importante, en razón a que permite a la empresa ampliar su efectividad y encausar proyecciones efectivas.
Objetivos
Objetivo general
Conocer y aplicar de manera efectiva los conceptos vistos en la unidad en resolución de problemas de contexto administrativo.
Objetivos específicos
- Conocer las técnicas de conteo y el uso de la probabilidad.
- Identificar y analizar los diferentes tipos de distribución de probabilidad.
- Describir los fenómenos aleatorios.
- Desarrollar la destreza necesaria para manejar aplicaciones de los conceptos de probabilidad.
- Interpretar y manejar las muestras aleatorias.
- Hacer cálculos con distribuciones de probabilidad.
- Inferir parámetros basados en distribuciones de probabilidad.
Técnicas de conteo
El principio de conteo es útil en la resolución de una cantidad de problemas. Tiene varias técnicas, como:
Conceptos básicos
La teoría de probabilidad moderna comenzó con un problema muy práctico: si un juego entre dos apostadores es interrumpido, el jugador con la ventaja tiene derecho a más de la mitad de la suma de dinero apostada, pero no a todo el monto. ¿Cómo dividir la ganancia? Este problema es considerado sin solución desde 1654, época en la cual un conde lo compartió con Blaise Pascal; sin embargo, su solución implica probabilidad.
El término probabilidad resulta familiar para la mayoría de las personas. Es común escuchar frases como “la probabilidad de la lluvia”, “la probabilidad de una inundación” y la “probabilidad de sacar cinco en la materia”. En palabras flexibles y cotidianas, la probabilidad indica un número que representa el grado de posibilidad de que ocurra algún evento o suceso en particular. Por ejemplo antes de lanzar una moneda, no se sabe con certeza el resultado; sin embargo, no existe duda que se deben considerar ambos resultados como igualmente posibles. Esto significa que la mitad de lanzamientos aparecerá cara; por lo tanto, la probabilidad de que ocurra cara en cualquier lanzamiento es 1/2 ó 50%.
Conceptos como espacios muestrales y eventos son importantes en el transcurso de esta unidad, cuyo conocimiento es la adecuada introducción al cálculo de probabilidades en problemas reales.
Probabilidad condicional
La probabilidad de un evento podría resultar afectada cuando se conoce la información adicional relacionada con el experimento. Por ejemplo, si trata de adivinar la respuesta a una pregunta de opción múltiple con cinco opciones, la probabilidad de obtener la respuesta correcta es 1/5. Sin embargo, si usted sabe que las respuestas A y B son erróneas (por tanto, pueden ser descartadas), adivinar la respuesta correcta se incrementa a 1/3.
Este tema considera situaciones similares en las cuales se busca la probabilidad de un evento A cuando se conoce que ha ocurrido otro evento B. Esto se llama una probabilidad condicional (denotada como P(A|B)) y se lee: “la probabilidad condicional de A, dado B”. Se halla por la fórmula:
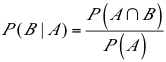
- Procesos estocásticos: eventos que tienen distintos resultados a pesar de suceder en las mismas condiciones y circunstancias.
- Eventos independientes: Cuando la información adicional no tiene efecto de un experimento con respecto a otro en una probabilidad condiciona, la probabilidad condicional P(A|B) y la no condicional P(A) son iguales; por tanto, se dice que A es independiente de B.
- Teorema de Bayes: método de aprendizaje probabilístico, que presenta dos etapas bien definidas, una de aprendizaje y otra de prueba (ver ejemplo).
Función de probabilidad
Distribución de una variable aleatoria: al igual que el caso unidimensional, una variable aleatoria bidimensional (X,Y) se caracteriza por su distribución; es decir, por el reparto de las probabilidades entre todos los valores (x, y) que tome. Esta distribución se representa mediante dos funciones, que asignan (de diferente forma) probabilidad a los valores que toma la variable:
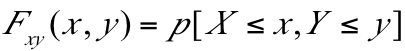
Función de probabilidad: si (X,Y) es una variable aleatoria bidimensional discreta, su función de probabilidad (f.p) en un punto (x,y) como:
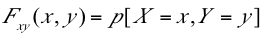
Esta función en el punto (x,y) toma la probabilidad de que ocurra X=x ; Y=y.
Para este tipo de variables se define la función de densidad conjunta (f.d.) como:
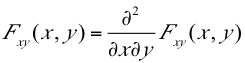
Variable aleatoria y distribución de probabilidad
Las variables aleatorias son aquellas cuyo valor depende del resultado de un proceso aleatorio; es decir, el valor que depende de la probabilidad cuyo resultado es un número asignado. Usualmente las variables aleatorias se simbolizan por letras mayúsculas X, Y o Z; mientras que sus valores respectivos, por letras minúsculas correspondientes. Por ejemplo: si una variable aleatoria es el lanzamiento de una moneda, el número de caras (X) que ocurren en el lanzamiento de dos monedas, los posibles valores se indican a escribir: X=x donde 1 y 2 son el resultado.
Son discretas si pueden asumir sólo un número finito de valores o en correspondencia uno a uno con los números enteros positivos. Se llama continua si pueden asumir cualquier valor en algún intervalo. Se consideran las probabilidades de eventos como 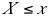 y
y  . Si X es discreta, la función f que asigna el número P(X=x) a cada valor posible de X, se llama la función de probabilidad o la distribución de la variable aleatoria X, así:
. Si X es discreta, la función f que asigna el número P(X=x) a cada valor posible de X, se llama la función de probabilidad o la distribución de la variable aleatoria X, así:
f(x)=P(X=x) se lee “f(x) es la probabilidad de que X asuma el valor de x”
Una distribución de probabilidad indica todos los posibles valores que puede tomar un experimento. Es semejante a la distribución de frecuencias relativas vistas en la unidad anterior; pero, en lugar de describir el pasado, describe la posibilidad de que un evento se realice en el futuro (como duración esperada, tiempo esperado, ganancia esperada, etc.). Constituye una herramienta potente para la proyección, en razon a que permite diseñar una serie de acontecimientos de acuerdo con las tendencias actuales de diversos fenómenos. Las decisiones estadísticas basadas en la estadística inferencial son fundamentales en la investigación, pues son evaluadas en términos de distribución de probabilidades. Una distribución de probabilidad muestra todos los resultados posibles de un experimento y la probabilidad de cada resultado.
Resumen
El concepto de probabilidad resulta familiar para cualquier profesional, pues involucra la toma de decisiones. Una definición más precisa considera la naturaleza matemática de dicho concepto.
Una definición frecuentista describe la probabilidad de ocurrencia de un determinado suceso como la proporción de veces que ocurriría dicha acción al repetir un experimento u observación en un número grande de ocasiones, bajo condiciones similares. Por definición la probabilidad se mide por un número entre cero y uno: si un suceso no ocurre nunca, su probabilidad asociada es cero; si ocurriese siempre, su probabilidad sería uno. Las probabilidades suelen venir expresadas como decimales, fracciones o porcentajes.
Un concepto más formal (desde el punto teórico) define la probabilidad mediante la verificación de ciertos axiomas, a partir de los que se deducen las demás propiedades del cálculo de probabilidades. Una interpretación más amplia incluye las probabilidades subjetivas o personales, las cuales expresan el grado de confianza o experiencia en una proposición. Esta definición constituye la base de los llamados métodos bayesianos (Teorema de Bayes), alternativa a la estadística tradicional, centrada únicamente en el contraste de hipótesis.
No obstante (en relación con el propósito de esta unidad) bastará con considerar las definiciones básicas, sin acudir a distribuciones de probabilidad de variables aleatorias, las cuales serán tratadas en la siguiente unidad. Es recomendable verificar los conceptos básicos de la probabilidad antes de hacer el cálculo de probabilidades, como las técnicas de conteo, operaciones y propiedades de la probabilidad, probabilidad condicional, tipos de variables aleatorias e introducción a función de probabilidad y distribuciones.
Bibliografía ()
- Berenson, M; Levine, D. (2001) Estadística para administración. 2ª edición. México. Editorial Prentice Hall.
- Canavos, G. (1987) Probabilidad y estadística: aplicaciones y métodos. México. Editorial Mc Graw Hill.
- Levin, R; Rubin, D. (2010) Estadísticas para administración y economía.. México. Editorial Pearson - Prentice Hall.
- Martínez, C. (2012) Estadística y muestreo. 13ª edición. Bogotá. Editorial ECOE.
- Mason, R; Lind, D. (2004) Estadística para administración y economía. 11ª edición. Bogotá. Editorial Alfa Omega.
- Mendenhall, W. (1990) Estadística para administradores. 2ª edición. México. Grupo editorial Iberoamérica.
- Milton, J; Jesse C. (2004) Probabilidad y estadística. 4ª edición. México. Editorial Mc Graw Hill
- Walpole, R; Meyers, R (2004) Probabilidad y estadística para ingenieros. 8ª edición. México. Editorial Prentice Hall.