La curva de isocuanta
En la economía, la curva isocuanta de producción, es, como lo dice su nombre, una curva en un espacio de insumos, que muestra todas las combinaciones posibles de trabajo y capital que se pueden generar dado un nivel determinado de producción (Isocuanta de producción, s.f.) .
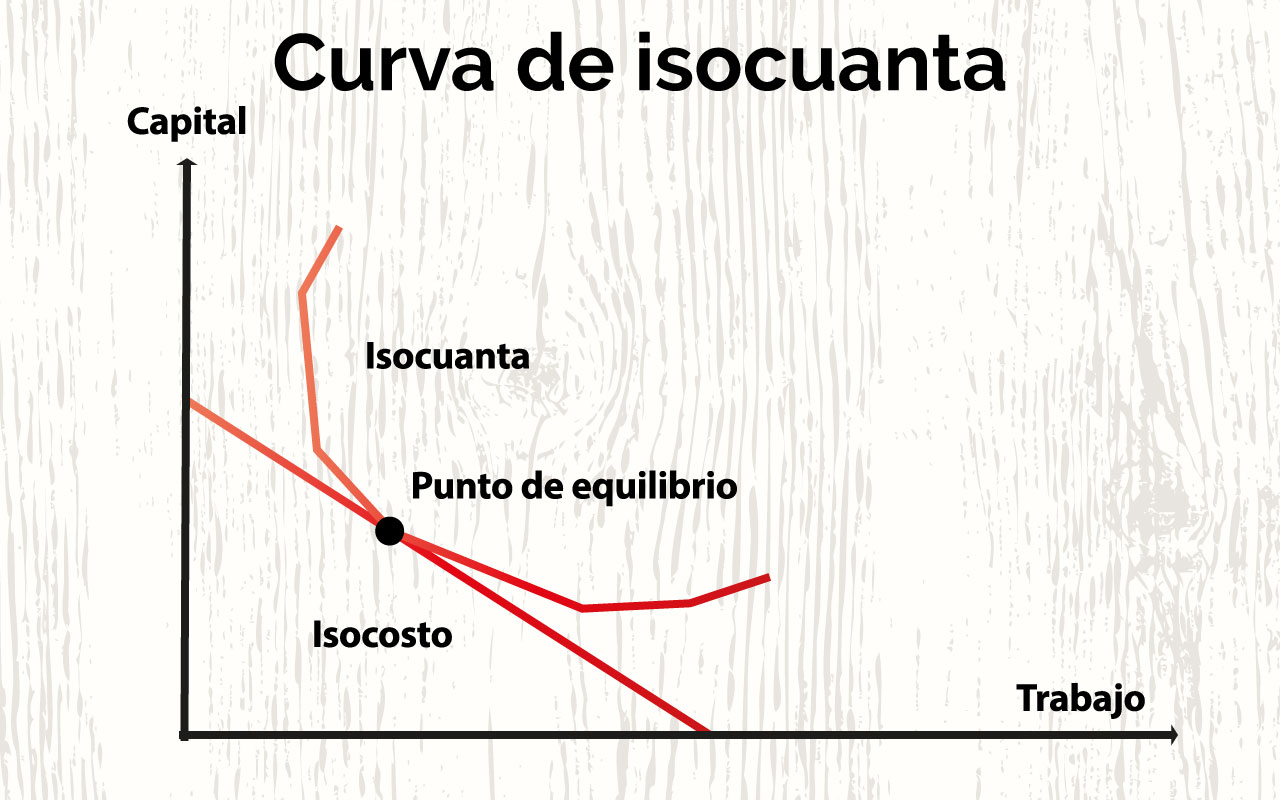
Tomando el ejemplo de la imagen, en el eje horizontal se miden los montos de trabajo, lo cuales se expresan en flujos de servicios por período de tiempo; a su vez, el eje vertical mide las cantidades de capital, mismas que son expresadas en flujos de servicio por período de tiempo.
La isocuanta de la imagen representa una tasa determinada de producción; así, cualquier combinación de capital y trabajo dada por un punto a lo largo de la isocuanta generará una cantidad de producción.
Conforme nos vamos moviendo sobre la curva, simultáneamente estamos cambiando las cantidades de los dos insumos capital y trabajo y las proporciones en las cuales estos son empleados (Isocuanta de producción, s.f.) .
Una curva isocuanta es el lugar geométrico que describe todas las combinaciones posibles de las cantidades de dos inputs o factores productivos variables que siguiendo una determinada tecnología le permiten obtener a la empresa una misma cantidad de producto. Para diferentes valores del output o cantidad de producto en la función de producción se obtiene una familia o mapa de curvas isocuantas. Las curvas isocuantas tienen las siguientes características: (Isocostos, 2013).
- Son decrecientes.
- Son convexas con respecto al origen de coordenadas.
- Indican mayor cantidad de producto cuanto más alejadas están del origen.
- No se cortan.
Curva que representa las combinaciones de cantidades de dos factores de producción con las que se obtiene la misma cantidad de producto.
Ruta de expansión
La ruta de expansión en un proceso de produccion la industria la logra al unir todos los posibles puntos de equilibrio que dan las diferentes isocuantas e isocostos alcanzados al modificar el gasto total, por lo que es similar a la gráfica de ingreso-consumo.
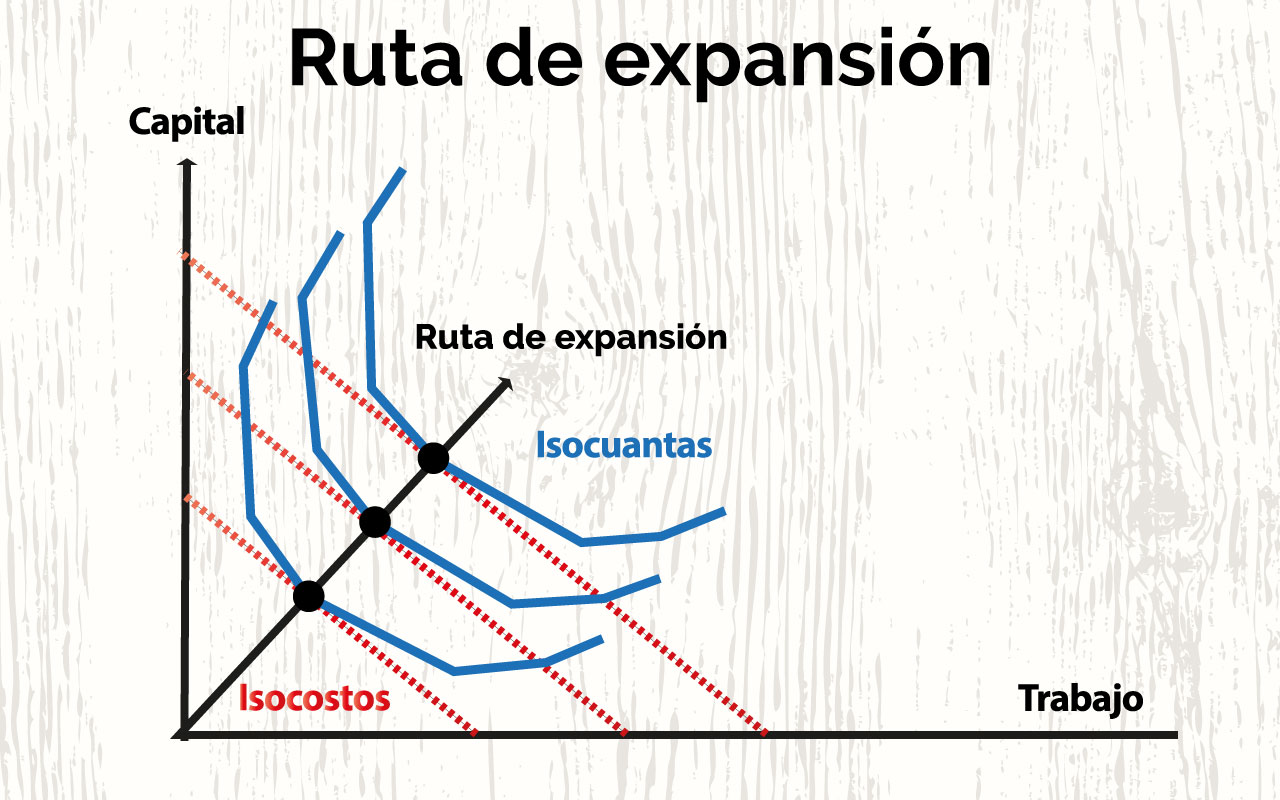
Fuente: Isocostos (2000).
Sobre un mapa de curvas isocuantas infinitamente denso, consideremos las diferentes rectas isocoste de equilibrio. De este modo, uniendo los diferentes métodos productivos eficientes técnica y económicamente obtendríamos la "senda de expansión de la producción".
A partir de los datos obtenidos de dicha senda, podríamos en el panel de la derecha representar los niveles de producción asociados a los diferentes costes totales. Para de este modo, uniendo dichos puntos, conseguir la curva de coste total a largo plazo.
Sustitución de factores
Al iniciar de una situación de equilibrio del productor el costo de un factor productivo desciende, cambiará su situación de equilibrio. Para establecer nuevamente el equilibrio, el productor reemplazará ese factor, por ahora relativamente más barato, de otro, hasta que el equilibrio se restituya. El nivel de posibilidad de sustituir capital por trabajo, como resultado por el cambio de precios relativos de los factores, se denomina elasticidad de la sustitución técnica, y se expresa como:
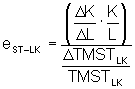
Isocuantas y la relación marginal de sustitución técnica (RMST)
En el reemplazo, los componentes de producción indican una igualdad en productividad; esto es, que la cantidad del factor que sustituye y el sustituido son igualmente productivos; es decir, dan el mismo nivel de producción.
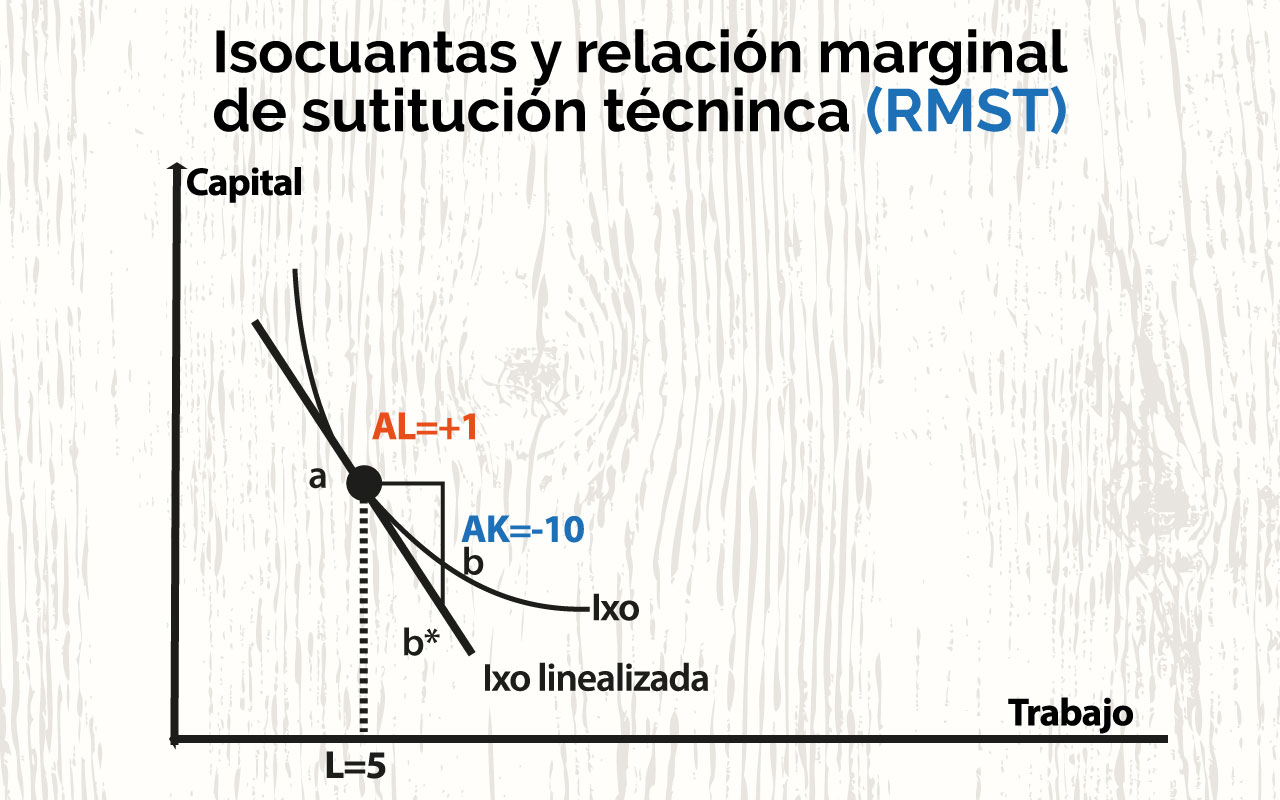
Fuente: Isocostos (2000).
Si la sustitución se expresa por unidad de uno de los factores en relación al otro, entonces, esta tasa de sustitución se denomina RMST. Ejemplo, la cantidad de capital que puede sustituir una unidad de trabajo manteniendo el mismo nivel de producción, es decir, sobre la misma isocuanta (ceteris páribus).
La RMST es la pendiente de la recta tangente a la isocuanta en cualquiera de sus puntos. La RMST es el fracción de los productos marginales de los factores Observe el paralelismo existente entre el equilibrio del productor a largo plazo y el del consumidor (isocuantas vs. Curvas de indiferencia; restricción presupuestaria vs. Isocoste)
La isocuanta al relacionar distintos métodos productivos que permiten obtener la misma cantidad de producto refleja situaciones tal como el método productivo A que implica más capital y menos trabajo si lo comparamos con el método productivo B.
La pendiente en un punto de la curva isocuanta se define como la Relación Marginal de Sustitución Técnica (RMST) entre capital y trabajo, o sea, cuántas unidades de capital se debe reducir con el fin de aumentar en una unidad el factor trabajo, para mantener el mismo nivel la producción.
Estimando que son muchos los nieles de producción que puedo considerar, infinitas serían las isocuantas que los constituirían. Si se toma un nivel de capital determinado K, podemos apreciar como a medida que nos movemos hacia la derecha en el plano cada isocuanta reflejaría un método productivo con la misma cuantía de capital, pero con más trabajo. De ahí, podemos deducir que en el mapa de isocuantas infinitamente denso, representaran mayor nivel de producción aquellas isocuantas situadas más alejadas del origen.
