Tipos de elasticidades de la demanda respecto al precio

Elasticidad demanda-precio

Es el cambio porcentual en la cantidad demanda ante un cambio del 1% en los precios; se la representa por el símbolo Epd y su fórmula es:

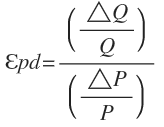
Donde:

ΔQ=Q.Final - Q.Inicial y
ΔP=P.Final - P.Inicial

Nota: Q= cantidad y P= precio.

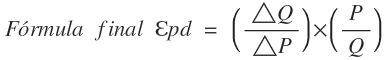
Debe señalarse que esta fórmula sirve para calcular la elasticidad precio en un punto de la función de demanda, pero arrojará error si lo que quiere medirse es la variación en un intervalo. Dado que la función de demanda tiene pendiente negativa, el valor de la elasticidad tendrá este signo y estará ubicado entre - ∞ y 0 (menos infinito y cero). Para facilitar la comprensión es usual trabajar la elasticidad en valores absolutos (Eumed, s.f.).

Usualmente, la elasticidad varía a lo largo de la función de demanda (existen funciones cuya elasticidad es constante; un caso interesante –aunque teórico- lo constituye la función de demanda de elasticidad constante unitaria (hipérbola equilátera a los ejes de coordenadas), cuya fórmula es Q = a. Pb; la elasticidad de la demanda es constante e igual a b.).

Considerando el valor absoluto, si es mayor que UNO la función es elástica, Pero es inelástica cuando el valor está entre cero y uno; es unitario cuando es igual a cero.

La elasticidad precio de la demanda está profundamente vinculada al dominio del efecto precio sobre la cantidad, o lo contrario: cuando la elasticidad es mayor a 1 (uno) –siempre en valores absolutos, si el efecto cantidad prevalece sobre el efecto precio; si la elasticidad es menor que uno, el efecto precio prevalece sobre el efecto cantidad.

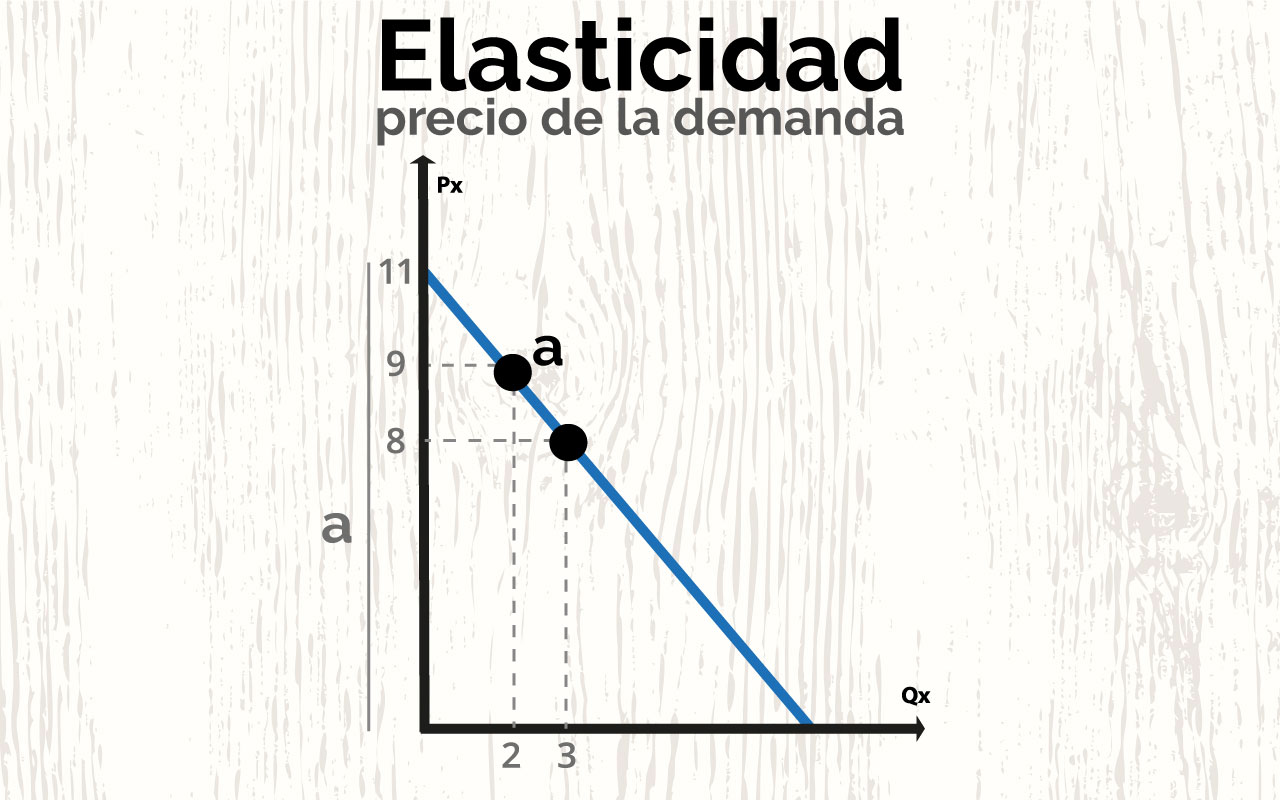
En los gráficos se da una relación entre la elasticidad en la función de demanda, la modificación en el ingreso total y el ingreso marginal:

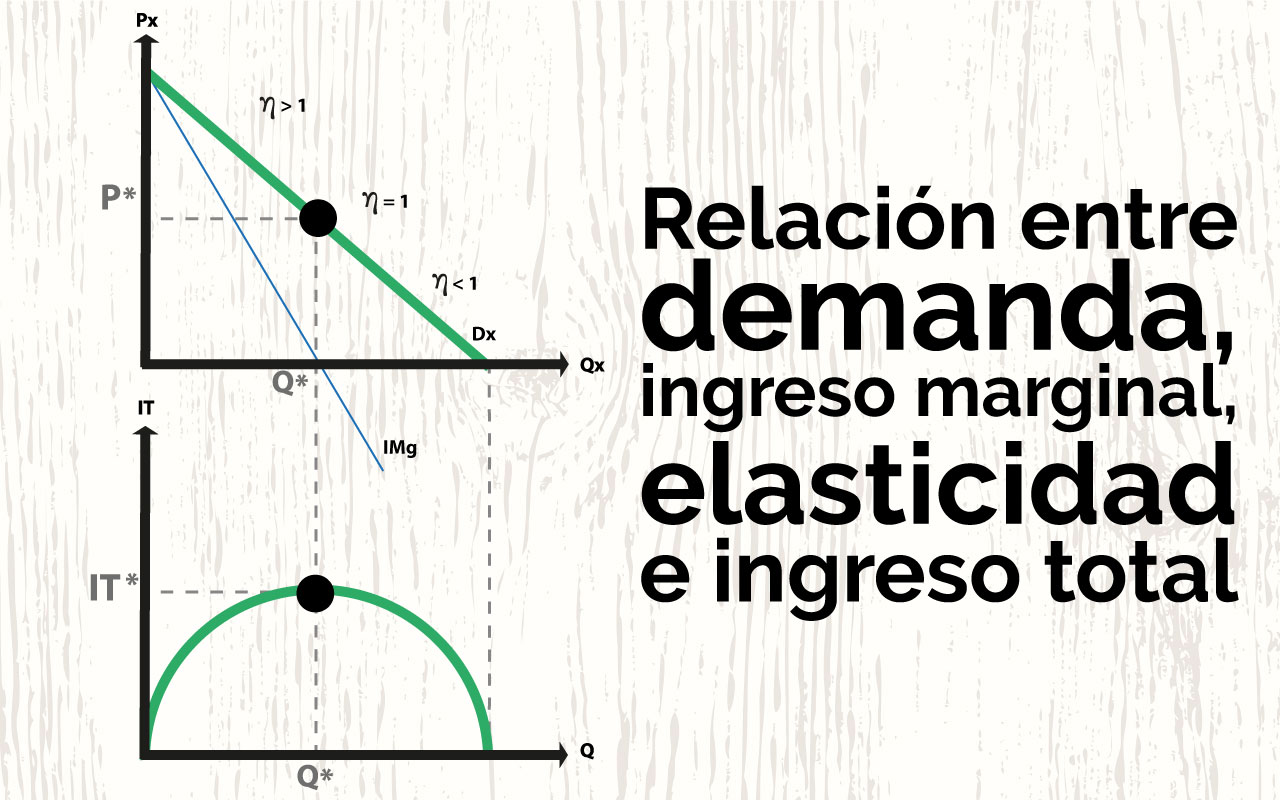
La función de demanda Dx representada en la parte superior del gráfico está dividida en tres zonas: zona elástica (E >1), zona de elasticidad unitaria (E = 1) y zona inelástica (E <1). El punto de elasticidad unitaria está determinado por P* y Q*. En la zona elástica, un descenso en el precio incrementará el ingreso total (gráfico inferior); este proceso puede continuar hasta alcanzar el punto de elasticidad unitaria, que coincide con el máximo ingreso total IT*, e iguala a cero el Ingreso marginal; a partir del punto de elasticidad unitaria, el descenso del precio reducirá el ingreso total (Eumed, s.f.).

(El razonamiento inverso es, por supuesto, igualmente válido: ubicados en la zona inelástica de la función, un aumento del precio incrementa el ingreso total, hasta alcanzar el punto de elasticidad unitaria).

Veamos un ejemplo de cálculo de elasticidad precio E en el punto α de la función de demanda de la Figura E7, que se corresponde a un precio de 9 y una cantidad de 2; utilizando la fórmula:

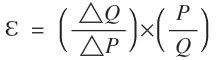
Siempre se calcula desde el punto inicial, o de partida); sustituyendo:

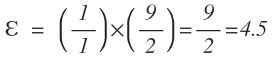
(La elasticidad precio en el punto α es de 4.5 (en valores absolutos).

Igualmente puede demostrarse que:

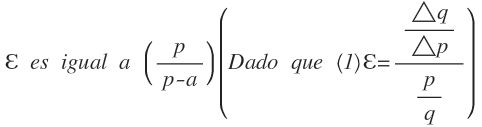
Y que la ecuación general de la recta es (2)p = a +bq. Entonces en (2):

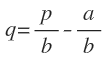
que sustituyendo en (1) nos queda:

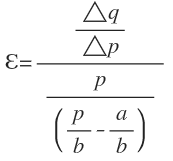
pero como:

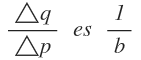
reemplazando y simplificando, tenemos:

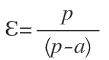
Fórmula muy sencilla, como vemos en el siguiente ejemplo, (el valor de a es la intersección de la función con el eje de las ordenadas):

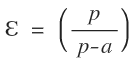
Sustituyendo:

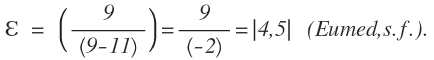
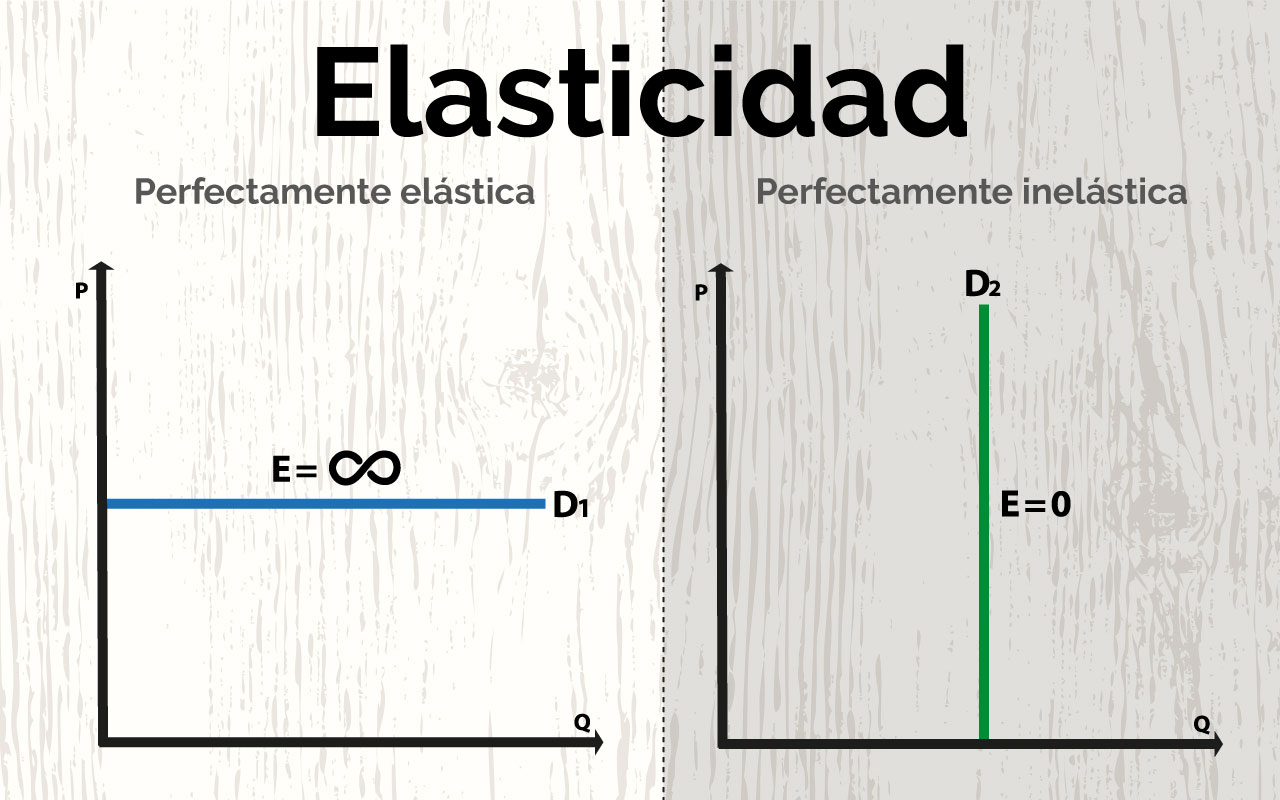
Como muestran los dos diagramas, la demanda perfectamente elástica se representa gráficamente como una línea horizontal y la demanda perfectamente inelástica, como una vertical. Estos son los únicos casos en los que tanto la EPD como la pendiente de la curva de demanda (ΔP/ΔQ) son constantes, así como los únicos casos en los que la EPD se determina solamente por la pendiente de la curva de demanda (o más precisamente, por la inversa de esa pendiente) (Elasticidad precio de la demanda, (2016).