La representación gráfica de la función cuadrática
Las parábolas
Son simétricas con respecto a una recta vertical llamado eje de simetría. El punto donde el eje de simetría corta a la parábola se llama vértice el cual se define: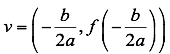 
Si a>0, el vértice es el punto más bajo de la parábola, esto significa que f(x) tiene un valor mínimo en ese punto, si a<0, el vértice es el punto más alto de la parábola, esto significa que f(x) tiene un valor máximo en ese punto.
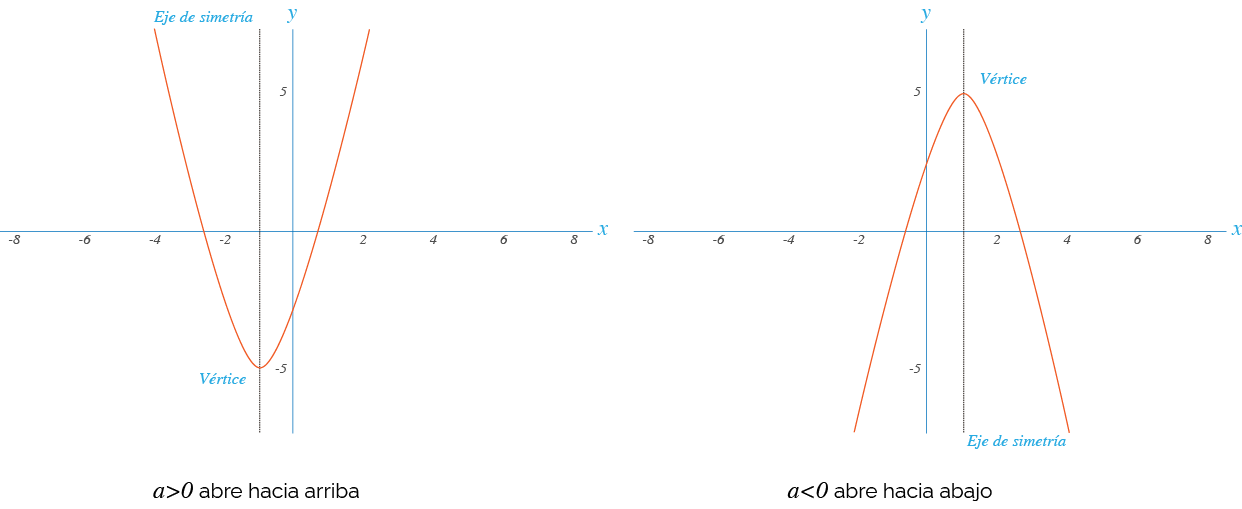
Ejemplo
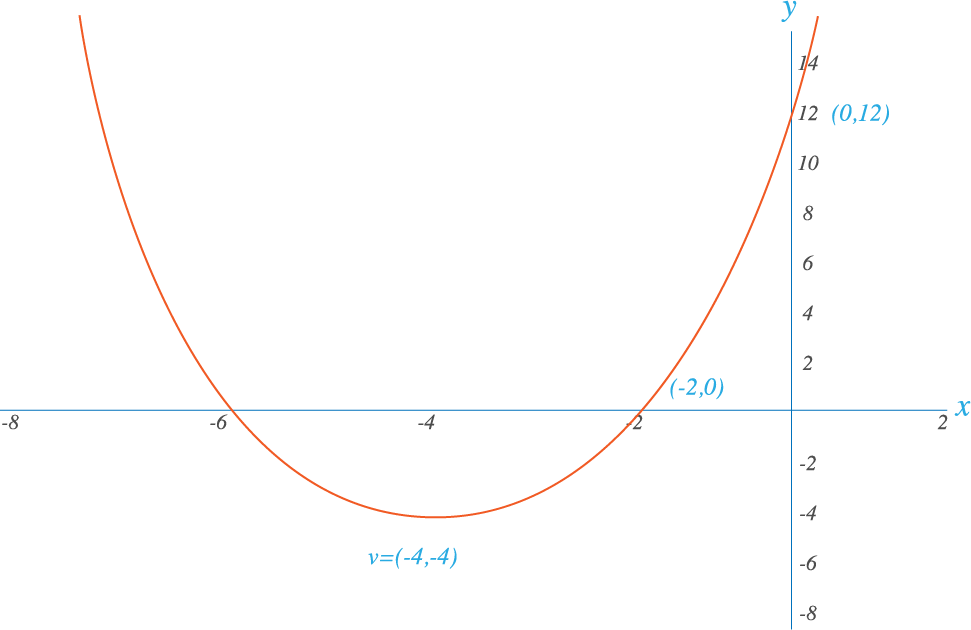
Graficar la función cuadrática y determinar el vértice, intersección con los ejes dominio y rango.
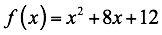
Solución
De la función a = 1, b = 8, c = 12 a>0 la parábola abre hacia arriba, el vértice es el punto más bajo lo que significa que hay un mínimo, la coordenada en el eje x del vértice es:
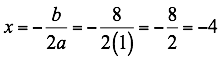
Sustituyendo en la función tenemos:
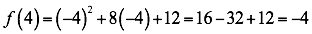Por lo tanto el vértice está en:
Para definir la intersección con los ejes coordenados en x se establece: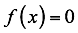 
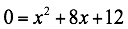
Utilizando la ecuación cuadrática tenemos, también se puede calcular por factorización.
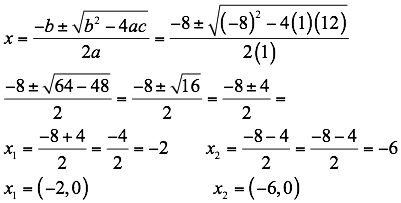
Para definir la intersección con los ejes coordenados en y se establece x = 0:
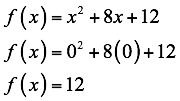
El dominio de una función cuadrática son todos los números reales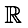 
, el rango se determina a través de la gráfica o desde el vértice hasta infinito [-4,∞ ]:
