Es la característica de la recta que hace referencia a su inclinación respecto al eje horizontal (x). Conociendo dos puntos tales como P1=(x1,y1) y P2=(x2,y2) sobre una recta no vertical definimos la pendiente como:
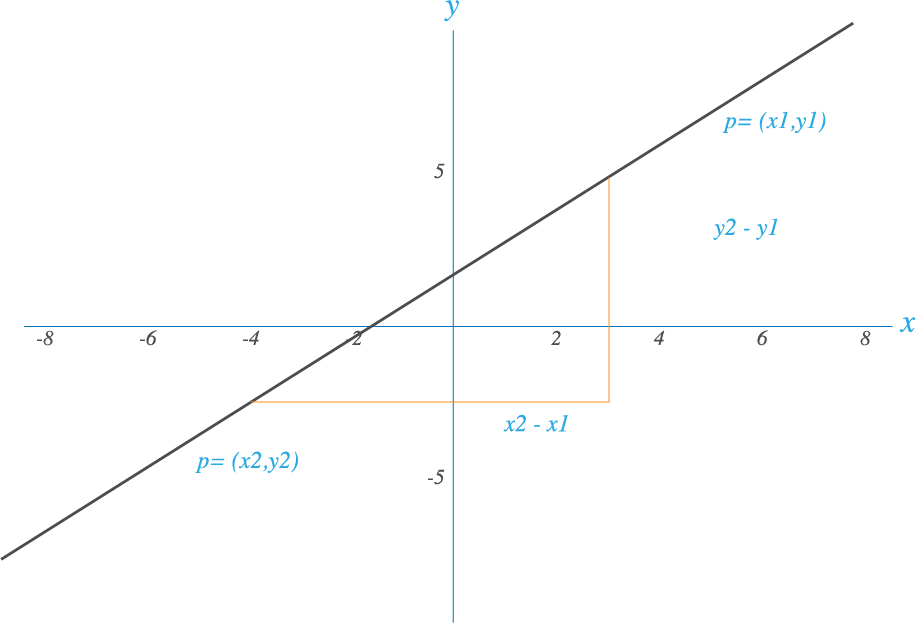
La orientación de la recta se caracteriza por su pendiente así:
La ecuación de una recta conociendo su pendiente m y un punto P1=(x1,y1) que pasa por ella y tomando un (x,y), el cual es otro punto de la recta, se puede hallar una relación de la ecuación de la recta llamada punto pendiente:
Determinar la ecuación de la recta que tiene pendiente m=3 y pasa por el punto p(2,3):
Solución
Utilizando la forma y-y1=m(x-x1) tenemos:
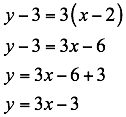
La cual se puede expresar 3x-3y-3. A esta la llamaremos pendiente-intersectó.
Determinar la ecuación de la recta que pasa p1=(2,-3) y p2=(5,4):
Solución
Se halla la pendiente de la recta a partir de los puntos dados, después sustituimos la pendiente y uno de los puntos en la forma punto pendiente:
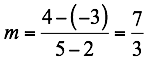
Tomamos la ecuación y-y1=m(x,-x1) con el punto p2=(5,4) y otro (x,y)así:
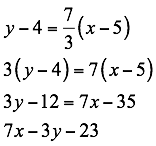
La gráfica representativa es:
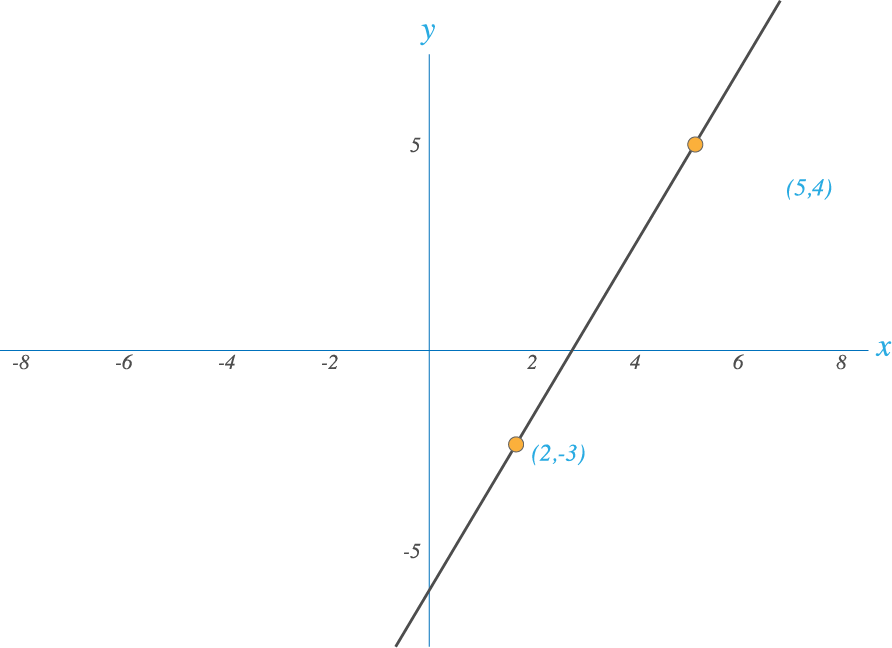
Es la ecuación de la recta con pendiente m e intersección en (y) igual a (0,b):
Determine la ecuación de la recta que satisfaga las condiciones dadas pasa por
p(5,-6) y p(4,-2). De la respuesta en forma pendiente intersecto.
Solución
Calculamos la pendiente entre los dos puntos, luego reemplazando en la ecuación de la recta la pendiente un punto en este caso p(4,-2) determinamos la ecuación solicitada.
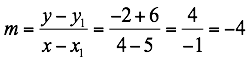
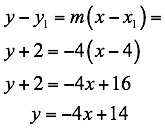
La ecuación solicitada es y = p(-4x+14) en forma pendiente-intersección.
Dos rectas son paralelas si y solo si tienen la misma pendiente.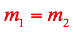 
Hallar la ecuación de la recta paralela a la ecuación dada
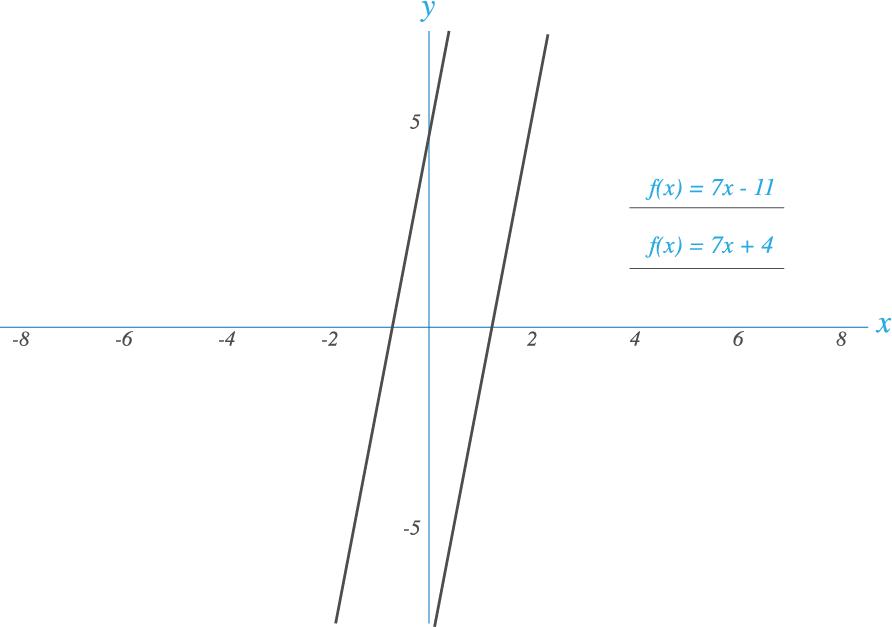
y = 7x+4 y pasa por (2,3):.
Solución
Tomamos la ecuación dada la cual está en la forma pendiente intersecto y = mx+b definimos a m1=7 la ecuación de la recta paralela tiene de pendiente m2=7:
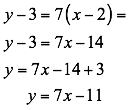
La ecuación solicitada es y = 7x-11 en forma pendiente-intersección:
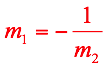
Dos rectas con pendientes 
y 
son perpendiculares si y solo si la pendiente de una es la recíproca con signo contrario de la otra.
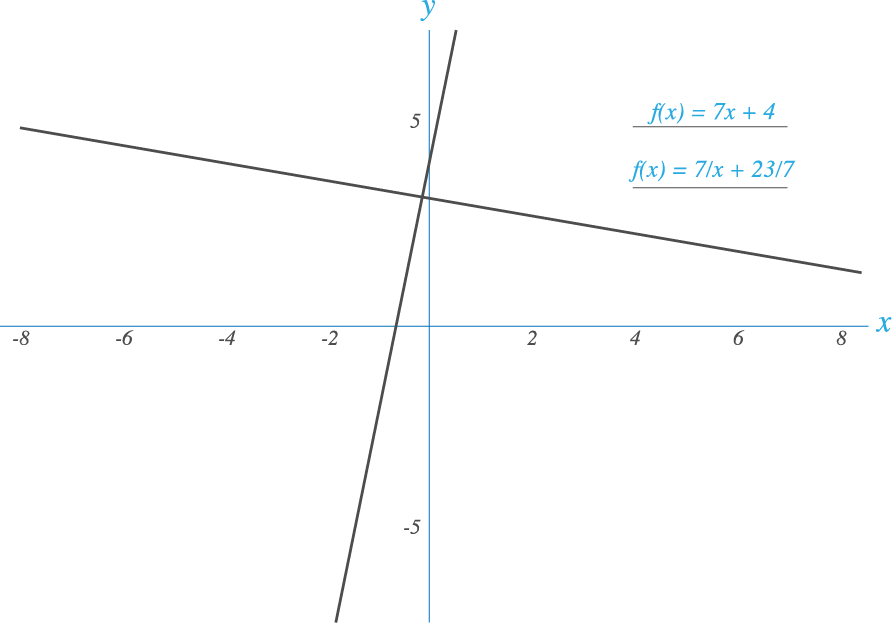
Hallar la ecuación de la recta perpendicular a la ecuación dada y = 7x+4 y pasa por (2,3):.
Solución
Tomamos la ecuación dada la cual está en la forma pendiente intersecto y = mx+b definimos a m1=7 la ecuación de la recta perpendicular tiene de pendiente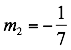 
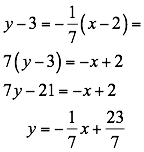
La ecuación solicitada es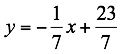 
en forma
pendiente-intersección:
