Aplicaciones de ecuaciones

Ejemplo 1

La compañía ALKON fabrica un producto para el cual el costo variable por unidad es de $ 12 y el costo fijo de $90.000, el precio de venta por unidad es de $17. Determinar el número de artículos que deben vender para tener una utilidad de $70.000.

Solución

Representamos la cantidad de unidades que se deben vender con la letra q, el costo variable será en pesos es 12q, los costos fijos $90.000, el costo total es 12q+90.000. El ingreso total es 17q además como:

Utilidad = ingreso total – costo total

El modelado para dar solución a este problema es:

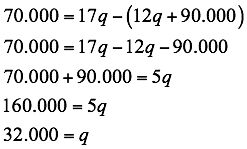
Para obtener utilidad de $70.000 se deben vender 32.000 unidades.

Ejemplo 2

Una compañía de bienes raíces es propietaria un conjunto de apartamentos, que comprende 96 pisos, un apartamento por piso. La renta es de $550 dólares mensuales y todos los apartamentos se ocupan. Sin embargo, por cada $25 dólares mensuales de aumento en la renta, se tendrán 3 apartamentos desocupados sin posibilidad de que se renten. La compañía quiere recibir $54.600 dólares mensuales de rentas, ¿cuál debe ser la renta mensual de cada apartamento?

Solución

Suponga que r es la renta que se cobrará por cada apartamento. Entonces el incremento sobre el nivel de $550 es de r-550. Como cada aumento de $25 causa que 3 apartamentos se desocupen, el número total de apartamentos vacantes será:

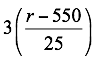
De aquí que el número total de apartamentos rentados será de:

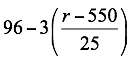
Como renta total=(renta por apartamento)(número de apartamentos rentados) se tiene:

Al resolver esta ecuación de segundo grado con la fórmula cuadrática se obtienen dos raíces:

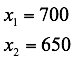
Así la renta de los apartamentos debe ser de $700 dólares o de $650 dólares.