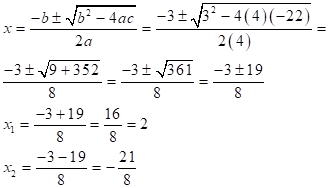Resuelve la ecuación cuadrática por factorización: 
El primer miembro de la ecuación se puede factorizar, así:
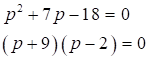Recuerde: Siempre que el producto de dos o más cantidades sea igual a cero, entonces, al menos una de ella es igual a cero; esto significa:
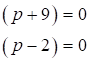Resolviendo estas ecuaciones se tiene:
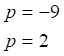Las cuales son las raíces de la ecuación original y su conjunto solución es:
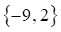
Resuelve la ecuación cuadrática por factorización: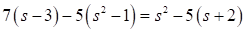 
Primero se multiplican los factores de cada miembro de la ecuación y se reducen términos semejantes, así:
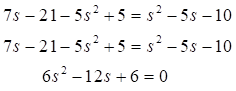Ahora la ecuación encontrada se puede factorizar, así:
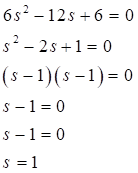Las cuales son las raíces de la ecuación original y su conjunto solución es igual:
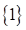
Resuelve la ecuación cuadrática por factorización: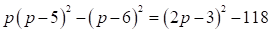 
Primero se multiplican los factores de cada miembro de la ecuación y se reducen términos semejantes, así:
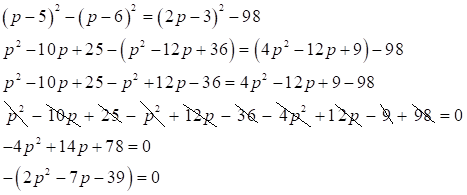Ahora la ecuación encontrada se puede factorizar, así:
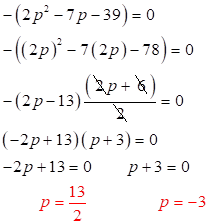Las raíces que satisfacen la de la ecuación original:
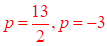Y su conjunto solución es: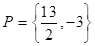 
Resuelve la ecuación fraccionaria que produce una ecuación cuadrática por factorización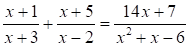 
Primero se multiplican los factores de cada miembro de la ecuación por el MCD, el cual es para ese caso:
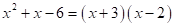Y se reducen términos semejantes así:
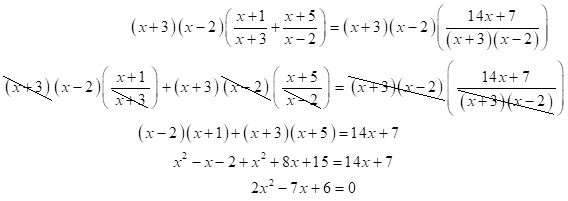Ahora la ecuación encontrada se puede factorizar así:
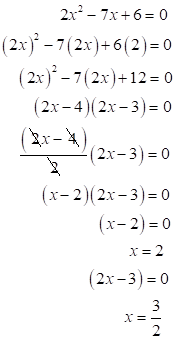Se demostró que si estos valores al ser sustituidos en la ecuación original son las únicas raíces posibles de la ecuación dada. Pero, al sustituir por 2 en la ecuación original produce en el denominador cero; entonces, 2 no es solución o de la ecuación y por lo tanto la única raíz: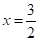 
Esta fórmula proporciona las raíces de cualquier ecuación de segundo grado en forma más directa, basta con aplicar dicha fórmula conociendo los valores de los coeficientes:
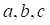De la ecuación:
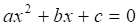La cual está dada por:
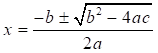
Resuelve la ecuación cuadrática utilizando la
fórmula cuadrática: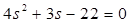 
Al aplicar dicha fórmula conociendo los valores de los coeficientes:
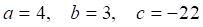De la ecuación dada tenemos:
