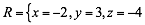Sistemas con tres variables
Los pasos para dar solución a un sistema de tres ecuaciones, con tres incógnitas, son:
- Se combinan dos ecuaciones dadas y se reduce una de las incógnitas, obteniendo una ecuación con dos incógnitas.
- Se combinan la tercera ecuación con otra de las ecuaciones dadas y se elimina la misma incógnita que se eliminó en el paso anterior, obteniendo otra ecuación con dos incógnitas.
- Con las dos ecuaciones obtenidas en los pasos anteriores, formamos un sistema de ecuaciones de dos incógnitas y por los métodos de reducción, sustitución, damos solución para encontrar el valor de una variable.
- Los valores obtenidos de las variables se reemplazan en una de las ecuaciones con tres incógnitas y determinamos el valor de la tercera variable.
Ejemplo
Resolver el sistema:
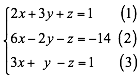
Combinamos la ecuación (1) y (2) y eliminamos la variable z, formando el siguiente sistema y obtenemos la ecuación (4)
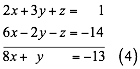
Combinamos ahora la ecuación (1) y (3) y eliminamos la variable z, formando el siguiente sistema y obtenemos la ecuación (5).
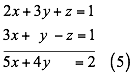
Ahora formamos un sistema con las ecuaciones (4) y (5) formando el sistema con dos incógnitas:
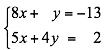
Resolviendo este sistema y eliminando a y, multiplicando la ecuación (4) por (-4) tenemos:
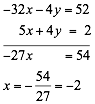
Sustituyendo la ecuación (5) tenemos:
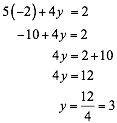
Sustituyendo y en cualquiera de las tres ecuaciones dadas ejemplo en (1) tenemos:
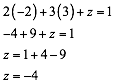
Entonces, la solución al sistema es: