División sintética

La división sintética cumple las siguientes reglas para obtener el cociente y el residuo de la división:

• El cociente siempre será un polinomio de un grado menor que el polinomio original.
• El coeficiente del término de mayor grado del polinomio original será el coeficiente del término de mayor grado del cociente.
• El coeficiente de un término cualquiera del cociente se obtiene multiplicando el coeficiente del término anterior, por el término independiente del binomio divisor, con el signo cambiado y este producto se le suma al coeficiente del polinomio original que está en la misma posición respecto al cociente.
• Para obtener el residuo de la división se multiplica el último coeficiente del cociente y se multiplica por el término independiente del binomio divisor con el signo cambiado y este producto se le suma al término independiente del polinomio original.

Ejemplo 1

Dividir x³-5x²+3x+14 entre x-3

Primero, se organizan los coeficientes del dividendo según sus exponentes y el segundo término del divisor con signo cambiado, así:

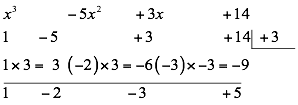
Luego de hacer la división, el resultado está en la parte inferior organizado de mayor a menor grado, y el último número es el residuo de la división. Entonces el resultado de la división es: -2x²-3x+5 Puesto que el residuo es diferente de cero, se deduce que x-3 no es múltiplo del polinomio en el dividendo.