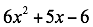Casos de factorización
Trinomios de la forma
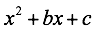
Se debe cumplir las siguientes condiciones:
- El coeficiente del primer término es 1, el primer término es una variable elevada al cuadrado.
- La variable del segundo término tiene la misma variable del primer término con exponente 1, con un coeficiente cualquiera.
- El tercer término es una cantidad cualquiera independiente de la variable.
Ejemplo 1
Factorizar
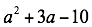
Procedimiento
Se factoriza el trinomio en dos factores (binomios), el primer término es la raíz cuadrada de:
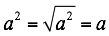
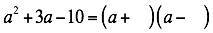
En el primer binomio el signo después de la variable es el signo del segundo término del trinomio en este ejemplo +, en el segundo binomio el signo es el producto del signo del segundo y tercer término del trinomio en este ejemplo (+.-=-)
Ahora hay que encontrar dos números que multiplicados sean igual al tercer término del trinomio y que sumados o restados según los signos sea igual al segundo término del trinomio. En este caso 5x2=10 y 5-2=3
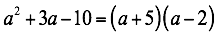
Ejemplo 2
Factorizar
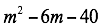
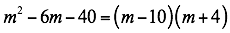
Trinomios de la forma
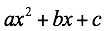
Este caso se diferencia del anterior porque el coeficiente de la variable al cuadrado es diferente de 1.
Ejemplo 1
Factorizar
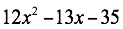
Procedimiento
Se multiplica el trinomio por el coeficiente de x2, dejando indicado el producto de segundo término, así 13(12x). Se obtiene:
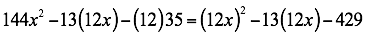
Luego descomponemos este nuevo trinomio teniendo en cuenta los procedimientos del caso anterior, así:
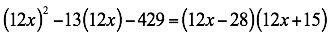
Como se multiplicó el trinomio debemos dividir los factores por el mismo valor para no alterar el trinomio dado, así:
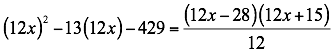
Pero ninguno de los binomios es divisible por 12. Entonces descomponemos a 12 en 4x3 =12 y tenemos:
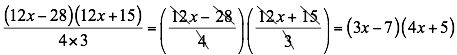
Ejemplo 2
Factorizar