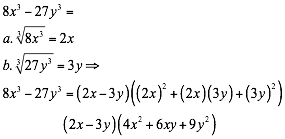Todos los términos del polinomio tiene un factor común.
Factorizar

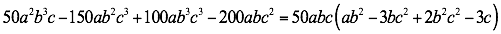 Ejemplo 2
Ejemplo 2
Factorizar
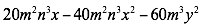
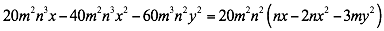
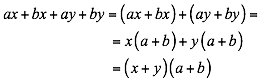 Ejemplo 1
Ejemplo 1
Factorizar
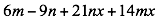
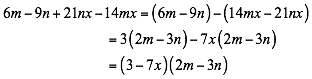 Ejemplo 2
Ejemplo 2
Factorizar
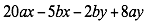
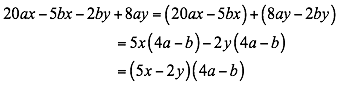
Ordene con relación a una letra, analicé el primer y tercer término. Son cuadrados perfectos si tienen raíz cuadrada exacta y positivos y el segundo término es el doble del producto de sus raíces cuadradas.
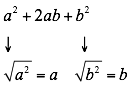
El segundo término es el doble del producto de estas raíces, así: 2 x a x b=2ab luego, el binomio calculado y separado por el signo del segundo término es:
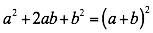
Factorizar
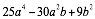
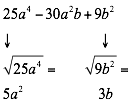
Comprobamos que el segundo término sea el doble del producto de las raíces:
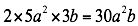
Entonces:
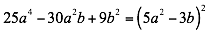
Factorizar
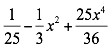
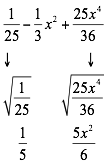
Comprobamos que el segundo término sea el doble del producto de las raíces:
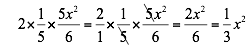
Entonces:
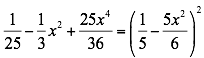
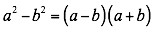
Se extrae la raíz cuadrada del primer término y del segundo término y se multiplican la suma por la diferencia de las raíces calculadas.
Ejemplo 1Factorizar
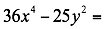
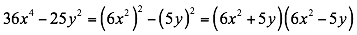 Ejemplo 2
Ejemplo 2
Factorizar
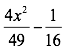
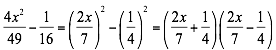
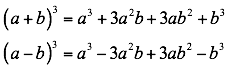
Para que una expresión algebraica sea el cubo de un binomio debe cumplir las siguientes condiciones:
Factorizar
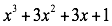
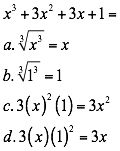
La expresión tiene cuatro términos y cumple con las condiciones dadas. Por lo tanto.
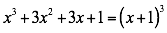
Factorizar
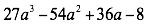
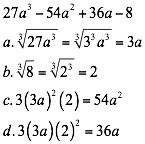
La expresión tiene cuatro términos y cumple con las condiciones dadas los signos que están intercalados más, menos se tiene.
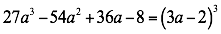
La suma de cubos perfectos se descompone en dos factores así:
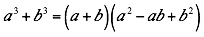
Ejemplo 1
Factorizar
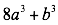
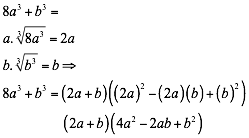
La diferencia de cubos perfectos se descompone en dos factores así:
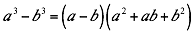
Ejemplo 1
Factorizar