Racionalizar un denominador
Se debe tener en cuenta que para eliminar una raíz cuadrada debe multiplicarse por otra igual, para que al quedar al cuadrado, se elimine el cuadrado con el índice de la raíz. También debe multiplicarse por esa misma expresión arriba y abajo; es decir, en el numerador y en el denominador, para no alterar la fracción.
En ocasiones, el denominador está expresado por un binomio, entonces se debe multiplicar por una expresión con diferente signo pero idéntica al binomio del denominador, dicha expresión se llama el conjugado del denominador.
Por ejemplo:
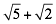
Tiene por conjugado:
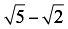
De manera que, al multiplicar estas dos expresiones, se tiene una diferencia de cuadrados que se resuelve restando el producto de los primeros términos de las dos expresiones, del producto de sus segundos términos, así:
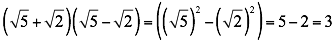
Ya que la raíz cuadrada se elimina con el cuadrado del exponente.
Para racionalizar esta expresión:
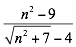
Se multiplica por el conjugado de la expresión que tiene el radical, es decir, por el denominador:
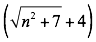
Conjugado:
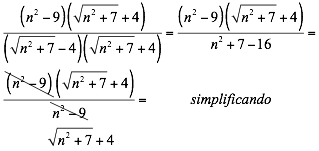
Esta última expresión es la respuesta racionalizada al ejercicio.
