Ejemplo desarrollado por diagramas de Venn y por fórmulas

En una encuesta realizada a un grupo de 104 estudiantes acerca de la música preferida se encontró que:

• Estudiantes que gustan del reguetón: 63.
• Estudiantes que gustan de la salsa: 54.
• Estudiantes que gustan de la música para planchar: 48.
• Estudiantes que gustan del reguetón y la salsa: 30.
• Estudiantes que gustan de la salsa y de la música para planchar: 25.
• Estudiantes que gustan del reguetón y la música para planchar: 26.
• Estudiantes que no les gusta ninguno de los tres géneros: 8.

Entonces, de acuerdo con lo anterior, ¿A cuántos estudiantes les gustan los tres tipos de música?

Supongamos que x representa el número de estudiantes que les gustan los tres tipos de música, luego:

30-x gustan únicamente de reguetón y salsa.

26-x gustan únicamente de reguetón y la de plancha.

25-x gustan únicamente de la salsa y la de planchar.

63 – (30-x) – (26-x) – x = x+7 gustan únicamente del reguetón.

54- (30-x) – (25-x) – x = x-1 gustan únicamente de la salsa.

48 – (26-x) – (25-x) – x = x-3 gustan únicamente de la de planchar.

Entonces (x+7) + (30-x) + (26-x) + (x-1) + (25-x) + (x-3) + x + 8 = 104.

De donde x + 92 = 104, entonces x = 12.

Luego a 12 estudiantes les gustan los tres tipos de música. Al sustituir el valor de x en cada una de las expresiones algebraicas del diagrama de Venn se obtiene la representación cardinal del conjunto de esta forma:

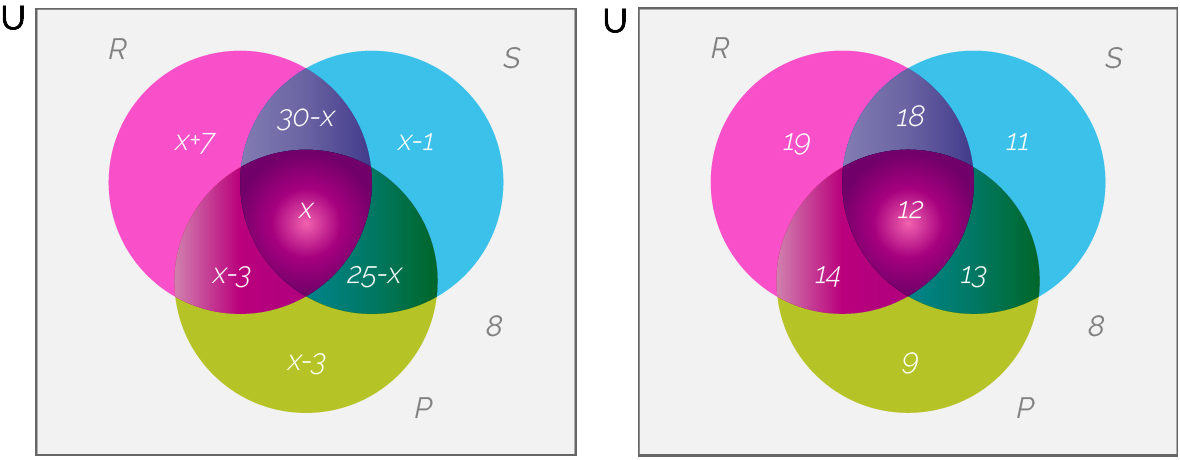
Fuente: Elaboración Propia.