Números racionales

Operación	Definición
Simplificación	Una fracción está reducida a sus términos más sencillos, o totalmente simplificada, cuando no hay ningún factor común al numerador y al denominador.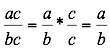
Multiplicación	El producto de dos fracciones algebraicas es otra fracción cuyo numerador y denominador son, respectivamente, el producto de los numeradores y el producto de los denominadores de las fracciones dadas. Es decir:
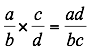División	El cociente de dos fracciones es igual al producto del dividendo por el recíproco del divisor; esto es:
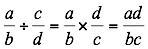Suma y resta	Si dos fracciones tienen denominador común, entonces su suma o diferencia se obtiene como: 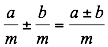Este método puede utilizarse para obtener la suma algebraica de tres o más fracciones que tengan un denominador común. Si dos o más fracciones no tienen un denominador común, entonces, pueden ser transformadas en otras fracciones equivalentes que sí lo tengan, lo cual permite operar como en el caso anterior. Si a yb son diferentes, entonces, 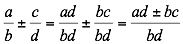Al transformar dos o más fracciones dadas en fracciones equivalentes con denominador común, conviene usar su menor denominador común; esto es el M.C.M. de los denominadores.