¿Cómo se determinan los valores de distribuciones de probabilidad?
Ejemplo
Un ingeniero informático necesita conocer el tiempo promedio que servirá un nuevo dispositivo. Mediante la prueba de la versión beta del mismo, pudo concluir que la función de distribución de probabilidad asociada a la variable aleatoria X corresponde a:
Calcular el valor esperado que obtiene el ingeniero y le permite conocer cuál debe ser la producción de los repuestos. Además, calcule la varianza de los datos.
Desarrollo
Por definición, el valor esperado corresponde a:
Es decir, el ingeniero puede esperar que el número de horas promedio que el dispositivo va a servir correctamente corresponde a 500 horas. Ahora, veamos qué tan dispersos se encuentran los datos, para esto, calculamos la varianza usando una identidad que permite simplificar algunas operaciones:
Así, la varianza sería:
Como la varianza es muy alta, significa que los datos están muy dispersos. Si vemos la gráfica de la función de distribución de probabilidades, es más sencillo entender esta medida de dispersión:
Función de distribución exponencial con media de 500 unidades.
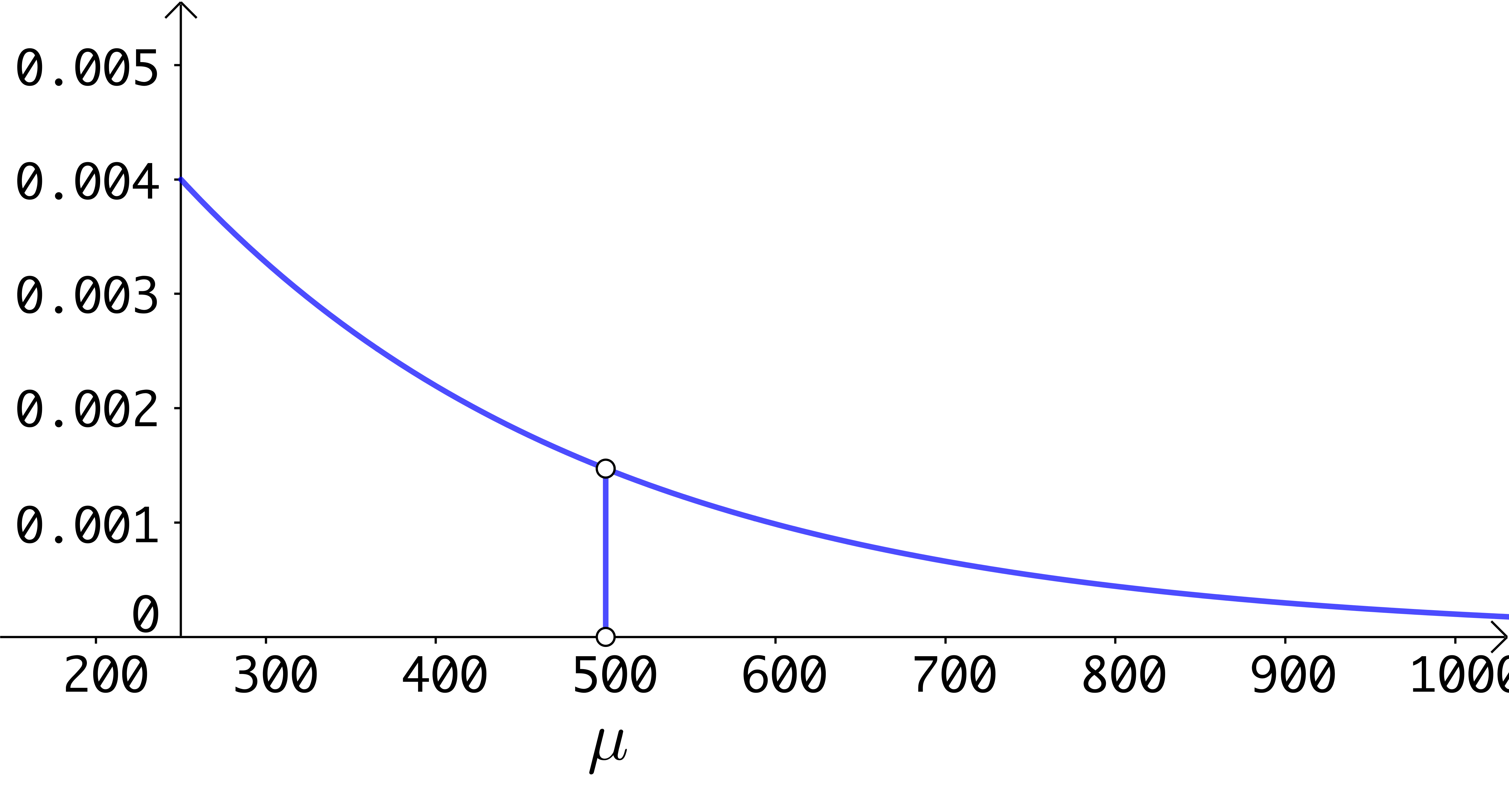
(Para ampliar la imagen haga clic sobre ella)
Como es posible visualizar en la gráfica anterior, la “mitad” de los datos están antes de 500, es decir, relativamente cerca, pero después de 500, se encuentra la otra “mitad” de los datos, estos pueden alejarse infinitamente, lo que implica que la varianza es muy alta.
