Ejemplo: personas esperando en una fila
Supongamos que elaboramos un modelo del número de personas que se encuentran haciendo fila en un supermercado para pagar sus artículos. Podríamos tener una variable que represente el número de personas por cada caja que estén esperando a ser atendidos. Suponiendo que hay tres cajas y en el peor de los casos, han estado 2 personas por cola, tendríamos los siguientes escenarios posibles:
Tabla 1.1: Escenarios posibles de personas esperando una fila.
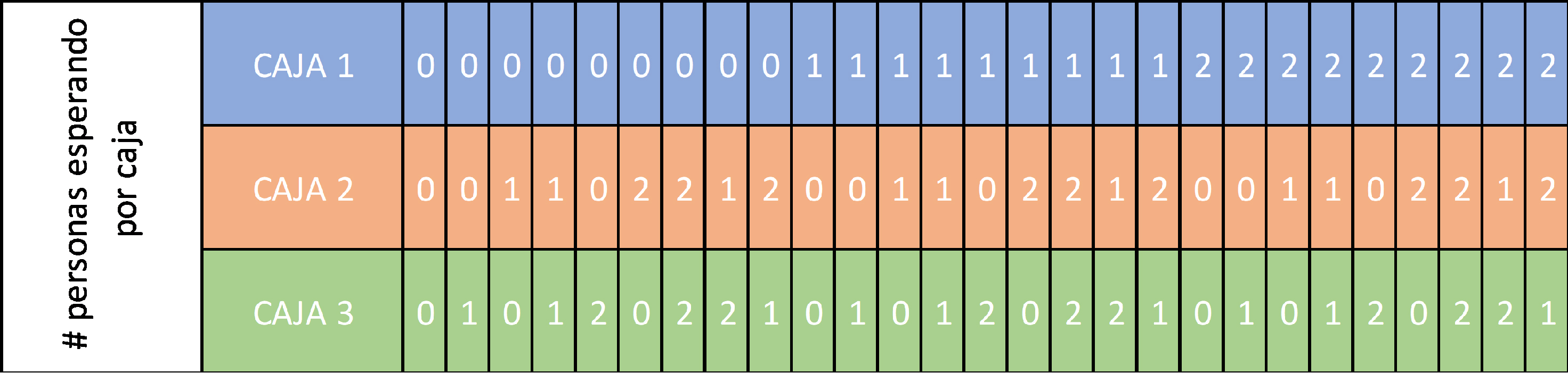
(Para ampliar la imagen haga clic sobre ella)
Estos posibles escenarios se conocen como el espacio muestral de un experimento y de acuerdo a lo que nos interese estudiar de este espacio muestral, podemos definir diferentes variables aleatorias. Veamos unos ejemplos:
- X = {# total, personas que están haciendo fila}.
- Y = {# cajas que tienen personas en espera}.
- Z = {# cajas libres}.
Cada una de estas variables aleatorias, permitirá asignar un valor real a cada uno de los posibles escenarios. Por ejemplo, con la variable aleatoria X, los siguientes escenarios {1,0,0}, {0,1,0}, {0,0,1}, que expresan de forma vectorial el número de personas que están haciendo fila para un cajero específico, por ejemplo, la terna {1,0,0} nos dice que hay 1 persona en la primera fila esperando ser atendida mientras en la fila 2 y 3, no hay personas en espera,. Para las tres ternas, la variable aleatoria X realiza una misma asignación correspondiente al valor 1. En el caso de la variable aleatoria Z, a todos los siguientes escenarios: {1,1,1}, {2,1,1}, {1,2,1}, {1,1,2}, {2,1,2}, {2,2,1}, {1,2,2} y {2,2,2}, les será asignado el valor 0, pues no hay ningún cajero libre.
Según el tipo de asignación, diremos que la variable aleatoria es discreta cuando el número de casos es finito (como los ejemplos anteriores) o infinitos pero comparables con los números enteros, es decir, es contable.
