Teorema del muestreo

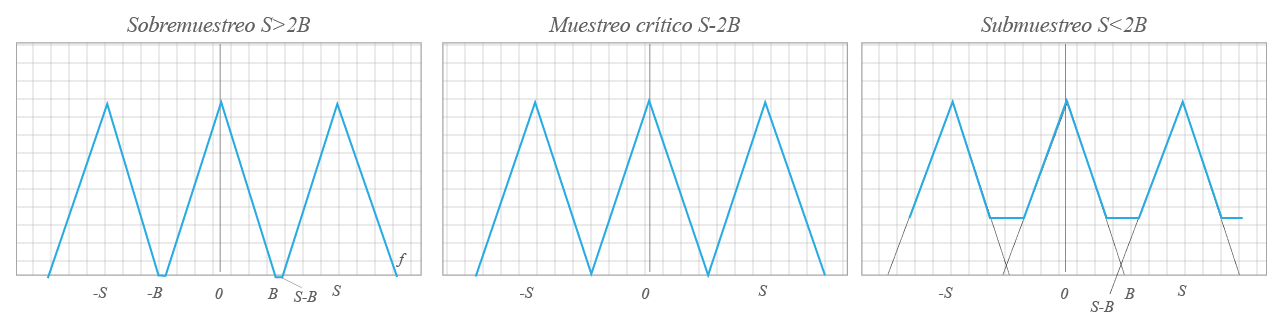
El Teorema del muestreo, dice que una señal analógica limitada en banda a una frecuencia B puede muestrearse sin pérdida de información, si la frecuencia de muestreo S es mayor que 2B (o si el intervalo de muestreo ts es menor que 1/2B). La frecuencia de muestreo crítica SN=2B a menudo se conoce como frecuencia de Nyquist o tasa de Nyquist y, el intervalo de muestreo crítico tN=1/SN=1/2B recibe el nombre de intervalo de Nyquist.

Las señales analógicas limitadas en banda pueden muestrearse sin pérdida de información. Si x(t) está limitada en banda a B, entonces para evitar la pérdida de información, la señal debe muestrearse a S>2B. Las imágenes de X(f) no tienen alias en el espectro periódico de XI(f) de la señal muestreada idealmente. La señal x(t) puede recuperarse exactamente a partir del periodo principal (-0.5S,0.5S) utilizando un filtro pasa-bajas ideal.

El submuestreo causa el alias espectral, el fenómeno de alias y la pérdida irreversible de información. Si S=2B, las imágenes de X(f) se traslapan en el espectro periódico y no es posible recuperar x(t). El fenómeno de alias se presenta cuando una frecuencia \left| {{f}_{0}} \right|>0.5S es suplantada por una frecuencia menor {{f}_{a}} en el intervalo (-0.5S, 0.5S).

Figura 3. Espectros de una señal limitada en banda.