Muestreo de señal x(t) e i(t)
Una señal muestreada puede ser definida como el producto de una señal analógica x\left( t \right) y un tren periódico de impulsos i\left( t \right).
La figura 1 muestra el producto de una señal continua análoga con un tren de impulsos. Esta señal muestreada puede ser descrita en forma matemática como:
La operación de muestreo conduce a una pérdida potencial de información en la señal muestreada en forma ideal XI\left( t \right), en comparación con su contraparte analógica x\left( t \right). Cuanto más pequeño sea el intervalo de muestreo {{t}_{s}}, menor será la pérdida de información. De cualquier manera, siempre existirá una pérdida de la misma.
Figura 1. Muestreo de señal x(t) e i(t).
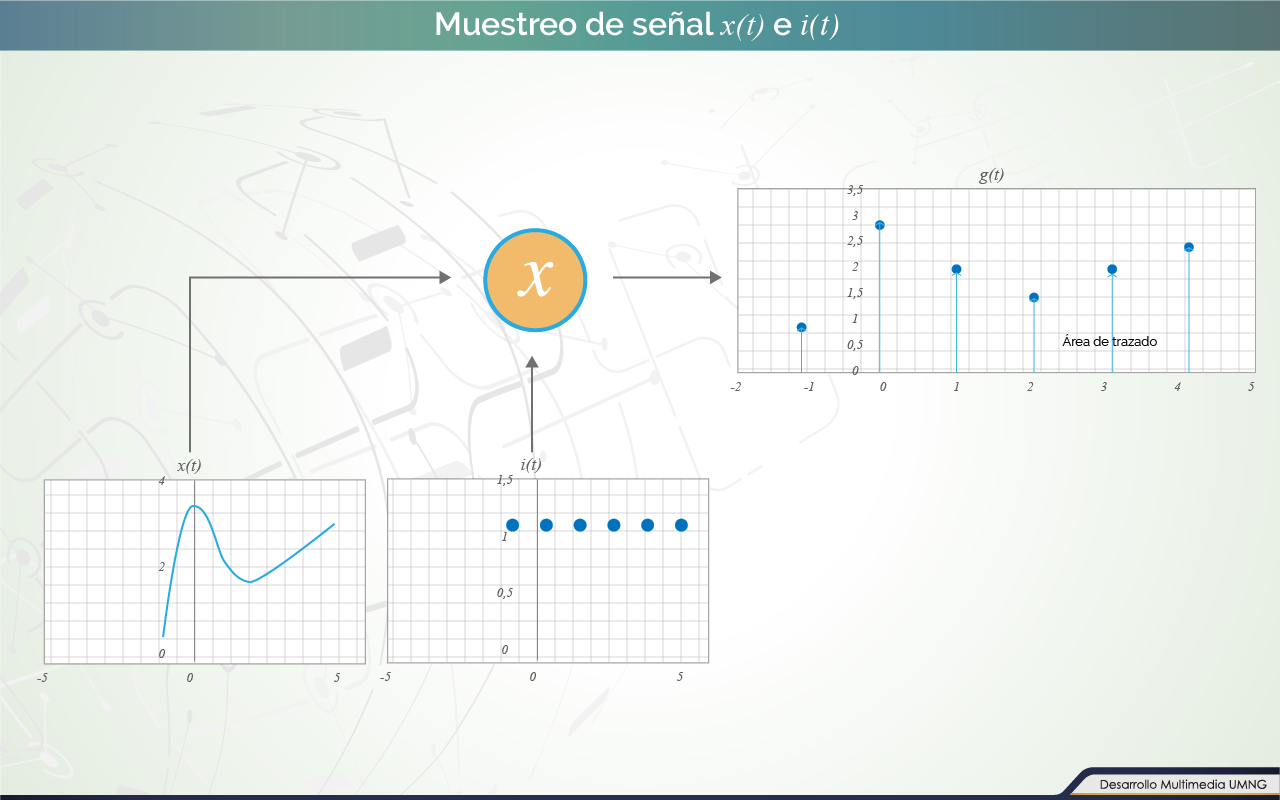
(Para ampliar la imagen haga clic sobre ella)
Para la señal muestreada que se ve en la gráfica de la Figura 2, se considera el tren de impulsos i\left( t \right) como una señal periódica con periodo T={{t}_{s}}=\frac{1}{S} y coeficientes de Fourier I\left[ k \right]=S. Su transformada de Fourier es un tren de impulsos (en f=KS) cuyas intensidades son iguales a I\left[ k \right]=S.
La señal muestreada idealmente XI\left( f \right) es el producto de x\left( t \right) e i\left( t \right). Por tanto, su espectro se describe por la convolución.
El espectro {{X}_{I}}\left( f \right) está formado por el espectro X\left( f \right) y sus réplicas desplazadas o imágenes. Es periódico respecto a la frecuencia, con un periodo igual a la frecuencia de muestreo S.
Figura 2. Convolución entre x(f) e i(f).
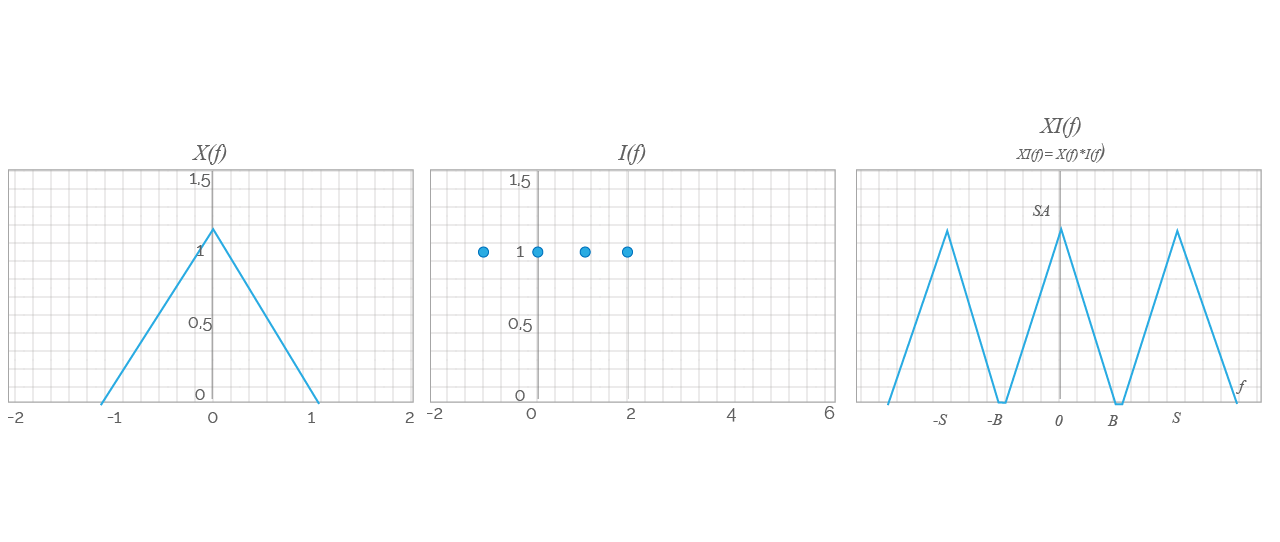
(Para ampliar la imagen haga clic sobre ella)
