Regresión de orden mayor

De manera similar a lo realizado en los casos de la regresión lineal y cuadrática, es posible extender el método para un polinomio de regresión de grado mayor.

En este caso, los residuos d_n se definen como:

{{d}_{1}}={{y}_{1}}-{{y}_{1}}'

{{d}_{k}}={{y}_{k}}-{{y}_{k}}'

Donde cada elemento y_k' se define como:

y_{1}^{'}={{a}_{n}}x_{1}^{n}+{{a}_{n-1}}x_{1}^{n-1}+{{a}_{n-2}}x_{1}^{n-2}+\ldots +{{a}_{2}}x_{1}^{2}+{{a}_{1}}{{x}_{1}}+{{a}_{0}}

y_{k}^{'}={{a}_{n}}x_{k}^{n}+{{a}_{n-1}}x_{k}^{n-1}+{{a}_{n-2}}x_{k}^{n-2}+\ldots +{{a}_{2}}x_{k}^{2}+{{a}_{1}}{{x}_{k}}+{{a}_{0}}

Así, redefiniendo los residuos, se obtiene:

{{d}_{1}}={{y}_{1}}-\left( {{a}_{n}}x_{1}^{n}+{{a}_{n-1}}x_{1}^{n-1}+{{a}_{n-2}}x_{1}^{n-2}+\ldots +{{a}_{2}}x_{1}^{2}+{{a}_{1}}{{x}_{1}}+{{a}_{0}} \right)

{{d}_{k}}={{y}_{k}}-\left( {{a}_{n}}x_{k}^{n}+{{a}_{n-1}}x_{k}^{n-1}+{{a}_{n-2}}x_{k}^{n-2}+\ldots +{{a}_{2}}x_{k}^{2}+{{a}_{1}}{{x}_{k}}+{{a}_{0}} \right)

Y la sumatoria de estos al cuadrado es:

\underset{i=1}{\overset{n}{\mathop \sum }}\,d_{i}^{2}=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\left( {{y}_{i}}-y_{i}^{'} \right)}^{2}}=\underset{i=1}{\overset{n}{\mathop \sum }}\,{{\left( {{y}_{i}}-\left( {{a}_{n}}x_{i}^{n}+{{a}_{n-1}}x_{i}^{n-1}+{{a}_{n-2}}x_{i}^{n-2}+\ldots +{{a}_{2}}x_{i}^{2}+{{a}_{1}}{{x}_{i}}+{{a}_{0}} \right) \right)}^{2}}

Donde n es la cantidad de puntos que se tienen como datos.

En este caso el problema se resume a calcular los valores de cada coeficiente a_k, que minimizan la función. Este es un problema que se puede resolver recurriendo a la derivación parcial de la función en términos de cada a_k, ahora, en ese orden de ideas, se llama F a la función a minimizar:

F=\sum {{\left( {{y}_{i}}-{{a}_{n}}x_{i}^{n}-{{a}_{n-1}}x_{i}^{n-1}-{{a}_{n-2}}x_{i}^{n-2}-\ldots -{{a}_{2}}x_{i}^{2}-{{a}_{1}}{{x}_{i}}-{{a}_{0}} \right)}^{2}}

Derivando la función respecto a cada a_k, se tiene:

\frac{dF}{d{{a}_{o}}}=2\sum \left( {{y}_{i}}-{{a}_{n}}x_{i}^{n}-{{a}_{n-1}}x_{i}^{n-1}-{{a}_{n-2}}x_{i}^{n-2}-\ldots -{{a}_{2}}x_{i}^{2}-{{a}_{1}}{{x}_{i}}-{{a}_{0}} \right)\left( -1 \right)=-2\sum \left( {{y}_{i}}-{{a}_{n}}x_{i}^{n}-{{a}_{n-1}}x_{i}^{n-1}-{{a}_{n-2}}x_{i}^{n-2}-\ldots -{{a}_{2}}x_{i}^{2}-{{a}_{1}}{{x}_{i}}-{{a}_{0}} \right) ( 1 )

\frac{dF}{d{{a}_{k}}}=2\sum \left( {{y}_{i}}-{{a}_{n}}x_{i}^{n}-{{a}_{n-1}}x_{i}^{n-1}-{{a}_{n-2}}x_{i}^{n-2}-\ldots -{{a}_{2}}x_{i}^{2}-{{a}_{1}}{{x}_{i}}-{{a}_{0}} \right)\left( -x_{i}^{k} \right)=-2\sum \left( {{y}_{i}}x_{i}^{k}-{{a}_{n}}x_{i}^{n+k}-{{a}_{n-1}}x_{i}^{n-1+k}-{{a}_{n-2}}x_{i}^{n-2+k}-\ldots -{{a}_{2}}x_{i}^{2+k}-{{a}_{1}}x_{i}^{1+k}-{{a}_{0}}{{x}_{i}}k \right) ( 2 )

Así, al reordenar las ecuaciones (1) y (2) y haciendo un proceso similar al realizado con las regresiones lineal y cuadrática, se obtienen las siguientes ecuaciones normales:

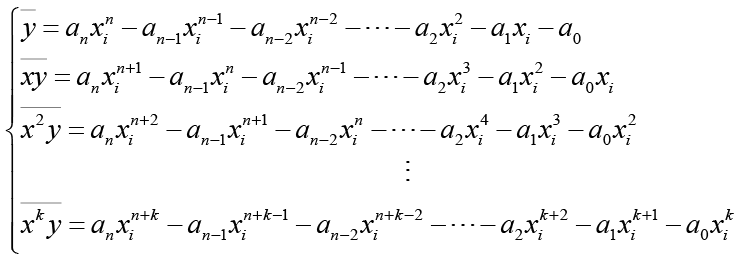
Al resolver este sistema de ecuaciones se obtienen los valores correspondientes para cada a_k, los cuales minimizan la función y permiten realizar la regresión polinómica. Recuerde que el valor máximo que puede tomar k es n.