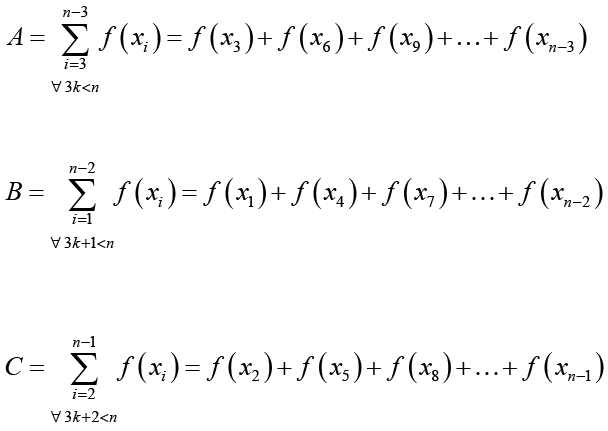Método de Simpson 3/8

Esta ecuación es conocida como método de Simpson 3/8 debido a que h se multiplica por 3/8. Se puede escribir de la forma:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \left( b-a \right)\frac{f\left( {{x}_{0}} \right)+3f\left( {{x}_{1}} \right)+3f\left( {{x}_{2}} \right)+f\left( {{x}_{3}} \right)}{8}

Además, este método se puede extender haciendo una partición del intervalo de integración en n subintervalos.

De tal manera, si se hace una partición del intervalo [a,b] en n subintervalos de anchura h=\frac{b-a}{n} se obtiene la partición \left\{ {{x}_{0}},~{{x}_{1}},~{{x}_{2}},~{{x}_{3}},~\ldots ,~{{x}_{n}} \right\}, siendo x₀=a y x_n=b.

Inmediatamente se evidencia que n debe ser un número múltiplo de tres para que efectivamente todo el intervalo [a,b] quede incluido. Entonces se obtiene:

\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx=\underset{a}{\overset{{{x}_{3}}}{\mathop \int }}\,f\left( x \right)dx+\underset{{{x}_{3}}}{\overset{{{x}_{6}}}{\mathop \int }}\,f\left( x \right)dx+\ldots +\underset{n-3}{\overset{b}{\mathop \int }}\,f\left( x \right)dx

Como se puede observar, en las integrales no se incluyen los puntos {{x}_{1}},~{{x}_{2}},~{{x}_{4}},~{{x}_{5}}\ldots ,~{{x}_{n-1}},~{{x}_{n-2}}, pues estos harán el papel de puntos tercios en cada uno de los intervalos.

Al sustituir la regla de Simpson 1/3 en cada integral, se obtiene:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{3h}{8}\left( f\left( {{x}_{0}} \right)+3f\left( {{x}_{1}} \right)+3f\left( {{x}_{2}} \right)+f\left( {{x}_{3}} \right) \right)+\frac{3h}{8}\left( f\left( {{x}_{3}} \right)+3f\left( {{x}_{4}} \right)+3f\left( {{x}_{5}} \right)+f\left( {{x}_{6}} \right) \right)+\ldots +\frac{3h}{8}\left( f\left( {{x}_{n-3}} \right)+3f\left( {{x}_{n-2}} \right)+3f\left( {{x}_{n-1}} \right)+f\left( {{x}_{n}} \right) \right)

Y de manera general se obtiene:

I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{3h}{8}\left( f\left( a \right)+2A+3B+3C+f\left( b \right) \right)

Siendo: