Método del trapecio compuesto
Para aplicar este método se debe tomar una partición \left\{ {{x}_{0}},~{{x}_{1}},~{{x}_{2}},~{{x}_{3}},~\ldots ,~{{x}_{n}} \right\} del intervalo [a,b], siendo a=x0 y b=xn. La partición debe ser equiespaciada de tal manera que:
{{x}_{i+1}}-{{x}_{i}}=h
\forall i\in \left\{ 1,~2~,~3,~\ldots ,n \right\}
Así, el valor de h será:
h=\frac{b-a}{n}
Ahora, si se tiene una integral definida y la partición establecida en el intervalo, se obtiene:
\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx=\underset{{{x}_{0}}}{\overset{{{x}_{1}}}{\mathop \int }}\,f\left( x \right)dx+~\underset{{{x}_{1}}}{\overset{{{x}_{2}}}{\mathop \int }}\,f\left( x \right)dx+\underset{{{x}_{2}}}{\overset{{{x}_{3}}}{\mathop \int }}\,f\left( x \right)dx+\ldots +\underset{{{x}_{n-1}}}{\overset{{{x}_{n}}}{\mathop \int }}\,f\left( x \right)dx
Y si se aplica el método simple a cada una de las integrales, se obtiene:
\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{h}{2}\left( f\left( {{x}_{0}} \right)+f\left( {{x}_{1}} \right) \right)+\frac{h}{2}\left( f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right) \right)+\ldots +\frac{h}{2}\left( f\left( {{x}_{n-1}} \right)+f\left( {{x}_{n}} \right) \right)
=\frac{h}{2}\left( f\left( {{x}_{0}} \right)+2\left( f\left( {{x}_{1}} \right)+f\left( {{x}_{2}} \right)+f\left( {{x}_{3}} \right)+\ldots +f\left( {{x}_{n-1}} \right) \right)+f\left( {{x}_{n}} \right) \right)
Obteniendo así la forma final del método del trapecio compuesto:
I\approx \underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \frac{h}{2}\left( f\left( {{x}_{0}} \right)+2\underset{i=1}{\overset{n-1}{\mathop \sum }}\,f\left( {{x}_{i}} \right)+f\left( {{x}_{n}} \right) \right)
Siendo:
h=\frac{b-a}{n}
Al igual que el método del trapecio simple, el del trapecio compuesto tiene una interpretación gráfica que se representa en la siguiente figura.
Método del trapecio compuesto
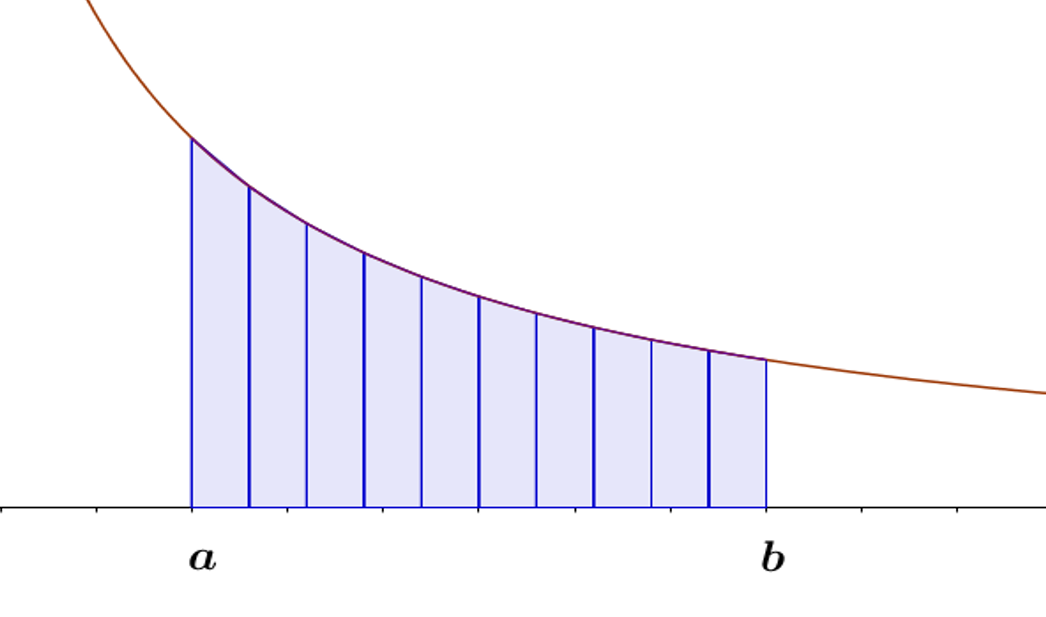
(Para ampliar la imagen haga clic sobre ella)
