Método del trapecio
Para el caso específico del método trapecio la cantidad de subintervalos es uno, luego n=1. Así, el polinomio interpolante para el método del trapecio, siendo a0=a y a1=b, es:
f\left( x \right)\approx {{P}_{1}}\left( x \right)=\frac{x-b}{a-b}f\left( a \right)+\frac{x-a}{b-a}f\left( b \right);~~\forall x\in \left[ a,b \right]~
Obteniendo de esta manera una aproximación a la integral, pues:
I=\underset{a}{\overset{b}{\mathop \int }}\,f\left( x \right)dx\approx \underset{a}{\overset{b}{\mathop \int }}\,{{P}_{1}}\left( x \right)dx=\frac{b-a}{2}\left( f\left( a \right)+f\left( b \right) \right)
El nombre de este método se debe a la interpretación geométrica que se le puede dar a la formula. En definitiva, se trata de aproximar el valor de la integral I por el área del trapecio determinado por las rectas x=a y x=b, el eje de las abscisas y la recta determinada por los puntos (a,f(a)) y (b,f(b)), como se muestra en la siguiente figura.
Método del trapecio.
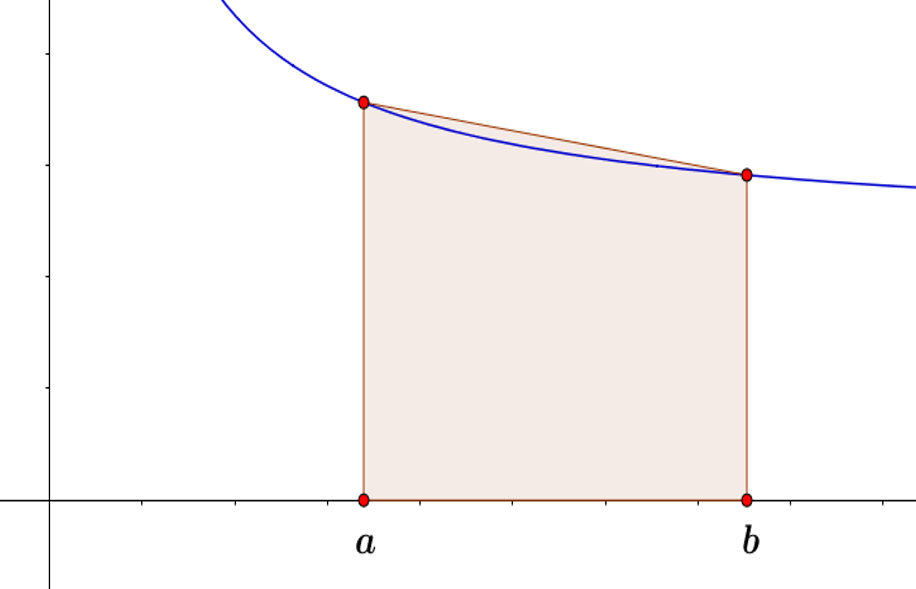
(Para ampliar la imagen haga clic sobre ella)
