Emparejamiento de coeficientes de las series trigonométricas de Fourier

Introducción

Entre los coeficientes que se muestran en el siguiente listado, determine cuál corresponde a cada una de las funciones 1, 2 y 3.

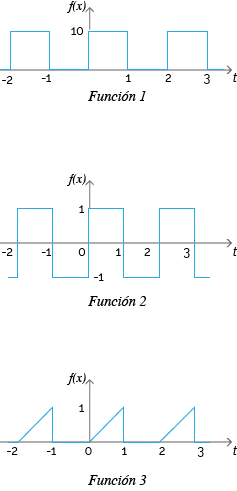
{{a}_{0}}=5 {{a}_{0}}=10 {{b}_{n}}=\frac{4}{n\pi } {{b}_{n}}=\frac{10}{n\pi } {{a}_{n}}=\frac{{{\left( -1 \right)}^{n}}-1}{{{(n\pi )}^{2}}~} {{a}_{n}}=\frac{{{\left( -1 \right)}^{n}}+4}{{{(n\pi )}^{2}}~}

Desarrollo

Para desarrollar la actividad se deben definir las funciones con los respectivos intervalos y determinar sus coeficientes remplazando los valores. Con la definición de estos valores se comienzan a evaluar los coeficientes partiendo de las siguientes ecuaciones:

{{a}_{0}}=\frac{2}{T}\underset{-\frac{T}{2}}{\overset{\frac{T}{2}}{\mathop \int }}\,f\left( t \right)dt~~~~~~~~~~~~~o~~~~~~~~~~~~~{{a}_{0}}=\frac{1}{T}\underset{0}{\overset{T}{\mathop \int }}\,f\left( t \right)dt~~~~ {{a}_{n}}=\frac{2}{T}\underset{-\frac{T}{2}}{\overset{\frac{T}{2}}{\mathop \int }}\,f\left( t \right)cos~\left( n{{\omega }_{0}}t \right)dt~~~~~~~~~~o~~~~~~~~~~~~~~{{a}_{n}}=\frac{2}{T}\underset{0}{\overset{T}{\mathop \int }}\,f\left( t \right)cos~\left( n{{\omega }_{0}}t \right)dt {{b}_{n}}=\frac{2}{T}\underset{-\frac{T}{2}}{\overset{\frac{T}{2}}{\mathop \int }}\,f\left( t \right)sen~\left( n{{\omega }_{0}}t \right)dt~~~~~~~~~~o~~~~~~~~~~~~~~{{b}_{n}}=\frac{2}{T}\underset{0}{\overset{T}{\mathop \int }}\,f\left( t \right)sen~\left( n{{\omega }_{0}}t \right)dt

A partir del siguiente procedimiento remplace los valores dados por medio del periodo y la amplitud de las funciones para obtener su respectiva solución. Por ejemplo, si desea encontrar el coeficiente {{a}_{0}}~de la función 1, deberá definir los intervalos de la función entre cero y uno, y entre uno y dos, donde se evidencian cambios de su amplitud o valor máximo, de la siguiente manera:

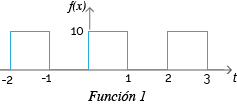
Entre cero y uno, los valores de la función son iguales a diez.

Entre uno y dos, los valores de la función son iguales a cero.

Para hallar el coeficiente {{a}_{0}} se remplazan los valores dentro de las ecuaciones como se muestra a continuación:

Así las cosas, hemos deducido que el coeficiente es igual a cinco; entonces, retomando el enunciado de la introducción, podremos responder que el coeficiente que corresponde a la función 1 es el a.

Para hallar el coeficiente {{a}_{n}} remplace los valores en las ecuaciones como se muestra a continuación:

Para hallar el coeficiente {{b}_{n}} remplace los valores dentro de las ecuaciones como se muestra a continuación:

A partir de esta metodología resuelva las dos funciones restantes desarrollando las integrales y haciendo uso de los conceptos vistos hasta este punto. Una vez concluido el ejercicio, socialice los resultados obtenidos con el tutor de la asignatura.