NÚMEROS BINARIOS

El sistema de numeración binaria que utiliza solo dos símbolos (0, 1). Se dice que tiene una base 2 y comúnmente se denomina sistema de numeración en base 2. A cada dígito binario se le denomina bit. En la siguiente tabla se ilustra el número binario y a la izquierda su equivalente en decimal:

Potencia de 2
Valor de la posición* 		24
16		 23
8		 22
4		 21
2		 20
1		 Número
decimal
El valor de la posición resulta de tomar la base 2 y elevarla a la potencia. Potencia cuyo valor depende de la posición del dígito que es tomada de derecha a izquierda e iniciando desde 0.
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
1
1
1
1
 
 
 
 
 
 
 
 
1
1
1
1
1
1
1
1
0
0
0
0
 
 
 
 
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
 
 
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Tabla 1. Tabla de números binarios con su equivalente en decimal (izquierda).

A partir de la tabla anterior, convertir el número 10110 es muy sencillo y se realiza de la siguiente manera:

Potencia de 2 24 23 22 21 20
Valor de la posición* 16 8 4 2 1
Binario 1 0 1 1 0
Decimal 16 0 4 2 0
Tabla 2. Conversión del número 10110 a decimal.

Y así sucesivamente hasta la operación con el último dígito binario.

Ahora cada resultado de las operaciones anteriores se suma para obtener el respectivo número decimal.

16 + 0 + 4 + 2+ 0 = 22

Considerar el número binario 1011011 para realizar el mismo procedimiento:

Potencia de 2 26 25 24 23 22 21 20
Valor de la posición* 64 32 16 8 4 2 1
Binario 1 0 1 1 0 1 1
Decimal 64 0 16 8 0 2 1

64 + 0 + 16 + 8 + 0 + 2 + 1 = 91

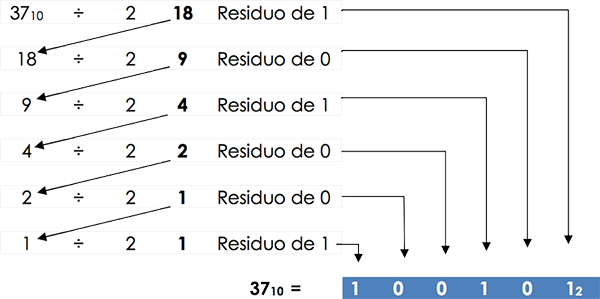
Tabla 3. Conversión del número 1011011 a decimal.

En el siguiente procedimiento se explica cómo convertir un número decimal a binario:

Considerar el No. 37:

Imagen 1. Conversión del número 37 a binario.