Retroalimentación Caso de estudio – Unidad 2
Aplicación de la regresión lineal para hacer una predicción
De acuerdo con cada literal planteado:
Con ayuda de Microsoft Excel se realiza el gráfico de dispersión de los datos:
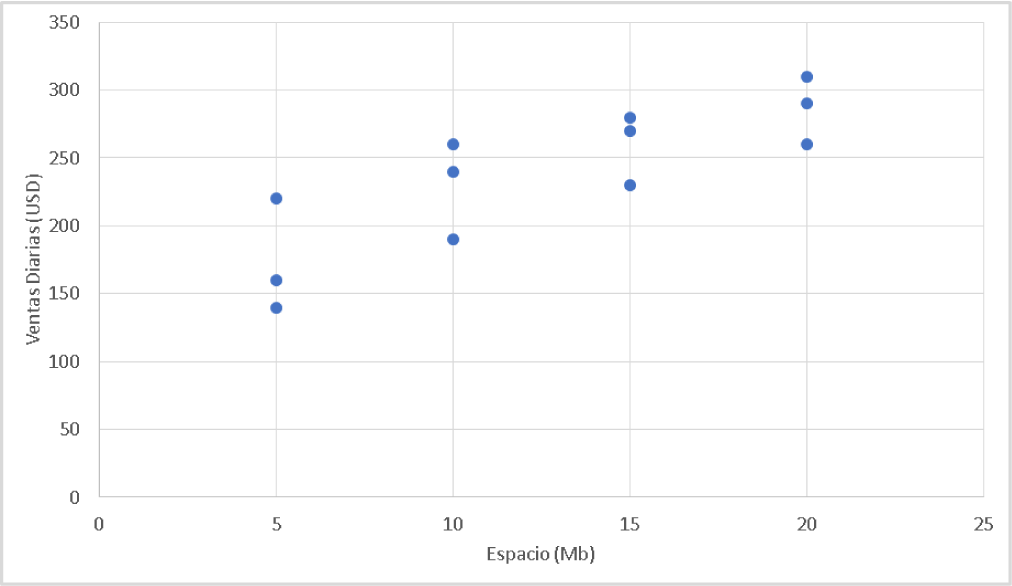
(Para ampliar la imagen haga clic sobre ella)
Para aplicar el método de mínimos cuadrados se deben realizar algunos cálculos previamente:
ESPACIO EN MEMORIA (Mb) X VENTAS SEMANALES (dólares) Y XY X2 Y2 Ŷ (Y - Ŷ)2 5 160 800 25 25600 182 484 5 220 1100 25 48400 182 1444 5 140 700 25 19600 182 1764 10 190 1900 100 36100 219 841 10 240 2400 100 57600 219 441 10 260 2600 100 67600 219 1681 15 230 3450 225 52900 256 676 15 270 4050 225 72900 256 196 15 280 4200 225 78400 256 576 20 260 5200 400 67600 293 1089 20 290 5800 400 84100 293 9 20 310 6200 400 96100 293 289 \sum X=150 \sum Y=2850 \sum XY=38400 \sum {{X}^{2}}=2250 \sum {{Y}^{2}}=706900 \sum {{(Y-\hat{Y})}^{2}}=9490
Para determinar los coeficientes de regresión se sustituye en las ecuaciones planteadas en la unidad de estudio:
a=\frac{\sum {{X}^{2}}~\sum Y-\sum X\sum \left( XY \right)}{n\sum {{X}^{2}}-{{(\sum {{X}_{i}})}^{2}}}=\frac{2250\left( 2850 \right)-150\left( 38400 \right)}{12\left( 2250 \right)-{{(150)}^{2}}}=145~USD
b=\frac{n\sum \left( XY \right)-\sum X\sum Y}{n\sum {{X}^{2}}-{{(\sum X)}^{2}}}=\frac{12\left( 38400 \right)-\left( 150 \right)\left( 2850 \right)}{4500}=7.40~USD/Mb
Por tanto, la ecuación de regresión está dada por:
\hat{Y}=145+7.4~X
La pendiente de la ecuación de regresión es el coeficiente b, en este caso 7.40 USD/Mb, lo cual quiere decir que por cada Mb que aumenta de espacio en el dispositivo se ganan 7.40 USD diarios.
Para hacer la predicción de las ventas diarias de una aplicación con 8 Mb de espacio ocupado en un dispositivo, se acude a la ecuación de la línea de predicción, ya que este dato no aparece explícito en la tabla proporcionada:
\hat{Y}=145+7.4~X
\hat{Y}\left( 8 \right)=145+7.4~\left( 8 \right)=204.20~d\acute{o}lares El error estándar de estimación se obtiene al resolver la siguiente ecuación:
{{s}_{yx}}=\sqrt{\frac{\sum {{(Y-\hat{Y})}^{2}}}{n-2}}\cong 30.80~d\acute{o}lares
Así se utilizará el modelo con los valores originales se tiene lo siguiente:
{{s}_{yx}}=~\sqrt{\frac{\sum {{Y}^{2}}-a~\sum Y-b\sum XY}{n-2}}=\sqrt{\frac{9490}{10}}~\cong 30.80~d\acute{o}lares
