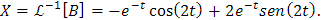La transformada de Laplace para algunos sistemas de ecuaciones que no son de primer orden

Sea

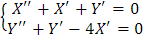
con condiciones iniciales X(0)=1,X' (0)=0,Y(0)=-1 e Y' (0)=5.

Aplicando la transformada de Laplace tenemos:

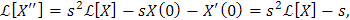
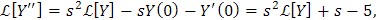
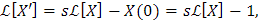
y

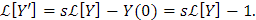
Si ponemos A=L[X] y B=L[Y], entonces al aplicar la transformada de Laplace al sistema dado y al reemplazar las expresiones calculadas anteriormente, obtenemos el sistema algebraico

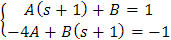
cuyas soluciones son

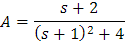
y

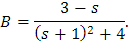
Finalmente, al calcular la transformada inversa de Laplace de A y B obtenemos que

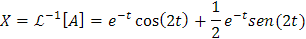
e