Cálculo de la solución particular por variación de parametros
Dado el sistema de ecuaciones X'=AX+G(t) de tamaño n×n, donde se conoce que la solución del sistema homogéneo X'=AX está dada por
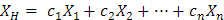
con
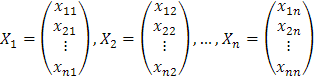
un sistema fundamental de soluciones, entonces al definir la matriz Φ(t) de tamaño n×n donde la columna i-ésima es igual al vector Xi, podemos escribir la solución Xc como Xc=Φ(t)C, donde C es el vector columna compuesto por los coeficientes c1, …, cn, es decir
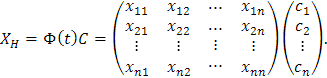
Está representación de la solución del sistema homogéneo, se realiza con el objetivo de generalizar el proceso de variación de parámetros visto en las primeras unidades, es decir que queremos encontrar una solución particular del sistema Xp a partir de reemplazar el vector numérico C por un vector de funciones C(t) en variable t y tomar Xp=Φ(t)C(t).
Si queremos que Xp sea una solución del sistema, entonces debe suceder que
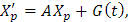
pero Xp'=(Φ(t)C(t))'=Φ'(t)C(t)+Φ(t)C'(t), donde Φ'(t) y C'(t) son las derivadas componente a componente de las matrices Φ(t) y C(t), respectivamente.
Ahora bien, como Φ(t) es una solución del sistema homogéneo (tomando el vector de coeficientes C igual al vector con todas sus componentes igual a 1), entonces se cumple que Φ'(t)=AΦ(t), de donde
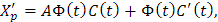
Así, reemplazando Xp=Φ(t)C(t) y la anterior expresión para Xp' en Xp'=AX_p+G(t), tenemos
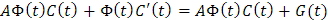
donde
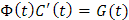
Si además tenemos en cuenta que los vectores X1,X2,…,Xn son linealmente independientes, es decir que su Wroskiano es diferente de cero para todo valor de t, entonces la matriz Φ(t) tiene inversa, que denotamos por Φ-1 (t).
Así, al multiplicar por Φ-1 (t) a la izquierda en Φ(t) C' (t)=G(t), llegamos a que
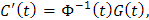
o equivalentemente, integrando componente a componente, a que
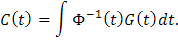
De ahí, podemos concluir que la solución particular Xp está dada por
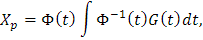
y que la solución total del sistema X'=AX+G(t) está dada por
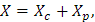
lo que se corresponde con lo ya explicado para la solución de ecuaciones diferenciales ordinarias lineales.
Ejemplo
Sea
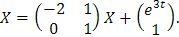
En la sección anterior vimos que el sistema homogéneo
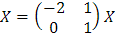
tiene como solución general

Luego en este caso
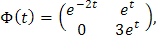
y su matriz inversa está dada por
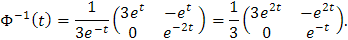
De ahí obtenemos que
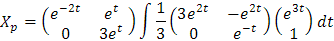
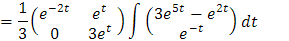
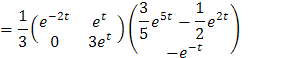

Finalmente, la solución total del sistema está dada por
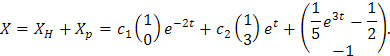
Si además a este problema agregamos la condición inicial
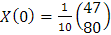
entonces se puede observar que la solución se obtiene tomando c1=1 y c2=3.
