Resumen del sistema homogéneo

Para resumir lo hecho podemos resaltar lo siguiente:

1. Para resolver el sistema X'=F(t)X+G(t) de tamaño n×n, tal vez con condición inicial X(t₀ )=X₀, primero debemos encontrar la solución del sistema homogéneo X'=F(t)X, lo cual se resume en encontrar un conjunto fundamental de soluciones X₁,X₂,…X_n, y luego debemos encontrar una solución particular X_p del sistema original. Así la solución total del sistema tendrá la forma

   

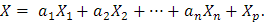
2. Hasta el momento hemos presentado las condiciones necesarias y suficientes para encontrar el conjunto solución del sistema homogéneo pero no hemos dicho cómo encontrar tal conjunto

   Así, el siguiente paso natural en nuestro proceso consiste en estudiar los mecanismos para encontrar tanto la solución del sistema homogéneo como la solución particular; sin embargo por la complejidad en el tipo de sistemas que puede aparecer, en principio nos centraremos solamente en estudiar la solución de sistemas normales de primer orden de ecuaciones lineales con coeficientes constantes.

Ahora bien, dependiendo del máximo grado de los operadores diferenciales que aparecen en F tenemos distintos tipos de sistemas. Particularmente en esta unidad nos centraremos en los sistemas de primer orden y para su solución recurriremos a herramientas de álgebra lineal como calculo matricial, calculo de determinantes, cálculo de autovalores y autovectores, entre otras.