Sistemas de ecuaciones diferenciales
La notación utilizada en la anterior definición es sugestiva y nos lleva a expresar tal sistema de ecuaciones en forma matricial como
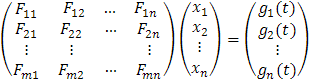
o

donde
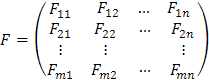
es una transformación lineal que transforma el vector
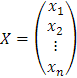
en el vector
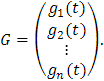
Claramente, la ecuación matricial (2), o equivalentemente el sistema (1), tiene solución si existe un vector de funciones X que satisfaga la ecuación.
Ahora bien, dependiendo del máximo grado de los operadores diferenciales que aparecen en F tenemos distintos tipos de sistemas. Particularmente en esta unidad nos centraremos en los sistemas de primer orden y para su solución recurriremos a herramientas de álgebra lineal como calculo matricial, calculo de determinantes, cálculo de autovalores y autovectores, entre otras.
