Operadores diferenciales lineales

Particularmente, nuestra intención es trabajar con operadores que se obtienen a partir del operador básico de derivación D como

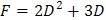
el cual toma a una función f(t) y genera como resultado la función

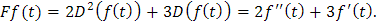
Sin embargo, debe observarse que para que tal transformación esté bien definida debemos asegurar que la función f(t) tenga tanto primera como segunda derivada y que tanto f'(t) como f''(t) estén definidas en un mismo dominio.

Así, dado un intervalo I del conjunto de números reales, denotamos por Cⁿ (I) al espacio vectorial de funciones reales que tienen derivada n-ésima continua en I y poniendo C₀ (I)=C(I).

Cuando se habla de números reales se incluye los intervalos de la forma (-∞,a) y (a,∞).