Transformada inversa de Laplace

En principio no podemos hablar de la transformada inversa de Laplace como tal, ya que la transformada de Laplace no es un operador uno a uno o inyectivo. Por ejemplo, si tomamos las funciones

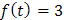y

fácilmente se observa que

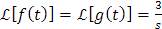
Sin embargo, gracias a un teorema de análisis, llamado teorema de Lerch, se puede concluir que si f y g son funciones continuas a trozos que están dominadas por una función exponencial y cumplen que sus respectivas transformadas de Laplace son finalmente iguales (es decir que existe algún real a tal que para s > a se tiene que L[f(t)](s) = L[g(t)](s)), entonces f(t)=g(t) para t > 0, salvo los puntos de discontinuidad. Así, bajo este resultado podemos decir que la transformada de Laplace de una función es esencialmente uno a uno, o de manera equivalente que la ecuación dada por

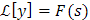
tiene esencialmente una única solución para y. A esta solución la denotaremos por

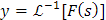
y de ahora en adelante la denominaremos transformada inversa de Laplace.

Claramente, por los resultados obtenidos hasta el momento conocemos las siguientes transformadas inversas de Laplace:

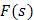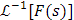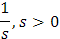	1
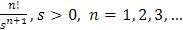
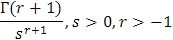
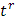
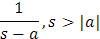
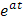
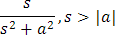
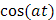
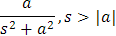
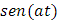
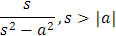
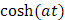
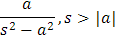
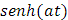
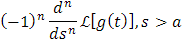
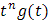
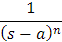
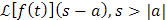
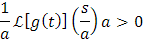
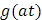
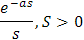
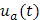