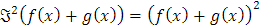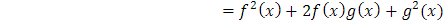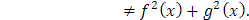Ejemplo de Operadores Lineales

1. Si tomamos A = B = FR y un número real fijo α, las funciones ℑ_α y ℑ² definidas como ℑ_α (f(x))=αf(x) y ℑ² (f(x))=(f(x))² son operadores.
2. Si denotamos por C al espacio vectorial real de las funciones reales diferenciables, entonces la clásica derivada D es un operador de C en FR que asigna a cada función diferenciable f(x) su derivada D(f(x))=f' (x).

Ahora bien, como en álgebra lineal general, nuestro interés se centra en los operadores lineales, es decir en aquellos operadores ℑ: A → B tales que para cualesquier par de funciones f(x), g(x) y cualesquier par de números reales a y b se cumple que

ℑ(af(x) + bg(x)) = aℑ(f(x)) + bℑ(g(x))

Este tipo de operadores son muy estudiados, ya que permiten estudiar las propiedades de un espacio vectorial con base en las de otro, además que facilitan ciertos cálculos pues permite una descomposición similar a lo que se logra con la propiedad distributiva de la multiplicación con respecto a la adición.

De los ejemplos anteriores, se observa que ℑ_α es un operador lineal ya que para f, g ∈FR y a,b ∈ R se tiene que

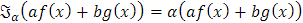
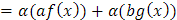
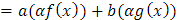
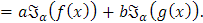
También, y gracias a las propiedades de la derivada se cumple que D es un operador lineal, pues para f, g ∈C y a,b ∈ R se tiene que

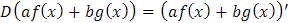
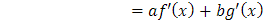
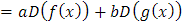
Sin embargo, se puede ver que ℑ² no es un operador lineal, pues para f,g ∈ FR se cumple que