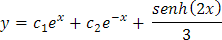Ejemplo de variación de parámetros

Resolver la ecuación diferencial

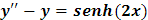
Paso 1: Resolver la ecuación diferencial homogénea asociada

La ecuación diferencial homogénea asociada es:

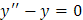
Ecuación auxiliar:

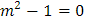
Si factorizamos la ecuación:

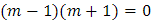
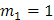y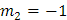

Por tanto, que la solución complementaria

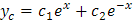
Paso 2: Formar los determinantes w, w₁, w₂

Recordemos que

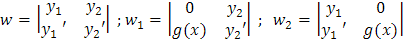
Ahora de la solución complementaria

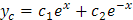
Identificamos a:

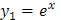y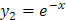

además:

y

y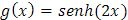

Luego que los determinantes están dadas por:

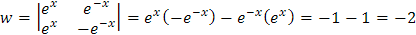
Ahora si hacemos uso de la definición del seno hiperbólico tendremos

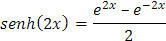
simplificamos:

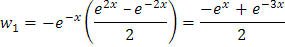
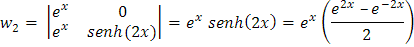
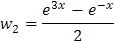
Paso 3: Escribir u₁' y u₂'

Ahora tenemos que:

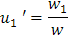y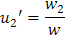

Con los resultados de la pestaña anterior tendremos:

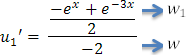
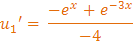
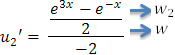
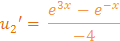
Paso 4:Integrar para calcular u₁ y u₂

Vamos ahora a integrar

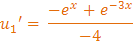y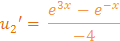

Iniciemos con u₁

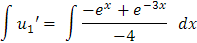
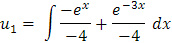
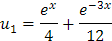
Y ahora para u₂

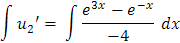
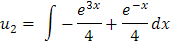
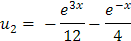
Paso 5: Solución Particular y solución general

Recordemos que la solución particular tiene la forma:

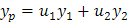
Luego en este caso se tenga:

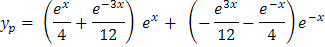
Al simplificar la solución particular y_p se tiene:

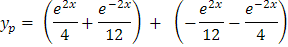
Asociando términos semejantes,

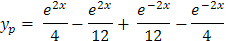
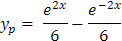
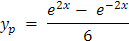
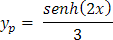
Y la solución general de la ecuación diferencial es: