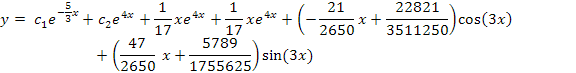Ecuaciones Diferenciales con Coeficientes Indeterminados
Ejemplo 1: Resolver la ecuación diferencial
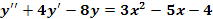
Paso 1: Resolver la ecuación diferencial homogénea asociada:
La ecuación diferencial homogénea asociada es:
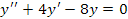
Ecuación auxiliar:

Si aplicamos la fórmula cuadrática tendremos:
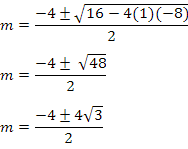
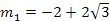 |
y | 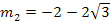 |
Por tanto, que la solución complementaria
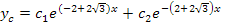
Paso 2: Suposición de la solución particular yp
Para ello identifiquemos
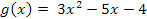
Luego la suposición sobre yp corresponde a:
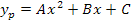
Paso 3: Calcular las derivadas yp'', yp'
La suposición de la solución particular de la ecuación diferencial es
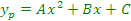
y las derivadas están dadas por:
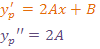
Y sustituyendo en la ecuación diferencial dada:
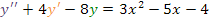
tendremos:
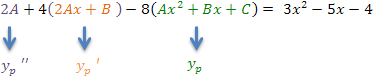
Simplificando la expresión:
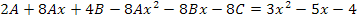
Agrupando términos semejantes:
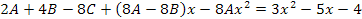
Paso 4: Establecer el sistema de Ecuaciones de los coeficientes
Ahora con la ecuación resultante del paso anterior:
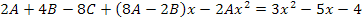
Establecemos la semejanza entre los términos de la ecuación así:
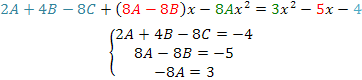
Al resolver el sistema de ecuaciones se tiene que:
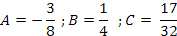
En consecuencia que la solución particular:
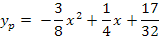
Paso 5: Solución General
Con la solución complementaria y la solución particular tendremos como solución general de la Ecuación diferencial:
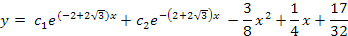
Ejemplo 2: Resolver la ecuación diferencial
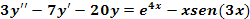
Paso 1: Resolver la ecuación diferencial homogénea asociada
La ecuación diferencial homogénea asociada es:
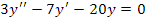
Ecuación auxiliar:
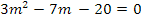
Si aplicamos la fórmula cuadrática tendremos:
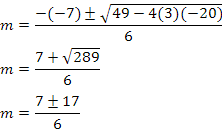
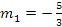 |
y | 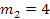 |
Por tanto, que la solución complementaria
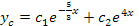
Paso 2: Suposición de la solución particular yp
Para ello identifiquemos
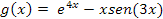
En este caso, g(x) está compuesto por la suma de una función exponencial e4x que le corresponde una suposión de la forma Ae4x pero observe que en la solución complementaria esta forma ya apareció c2e4x, por tanto se debe multiplica por el factor x la solución supuesta y quitar la dependencia lineal.
Luego que la suposición asociada a la forma e4x corresponde a Axe4x
Ahora para el segundo término del g(x) que tiene la forma de un producto entre una función lineal y una función trigonométrica, la solución supuesta corresponde a la forma
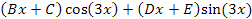
Quedando la solución yp de la forma:
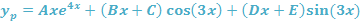
Paso 3: Calcular las derivadas yp'', yp'
La suposición de la solución particular de la ecuación diferencial es
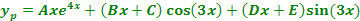
y las derivadas están dadas por:
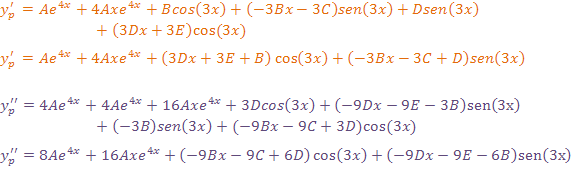
Y sustituyendo en la ecuación diferencial dada:
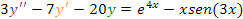
tendremos:
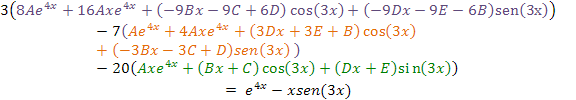
Simplificando la expresión:
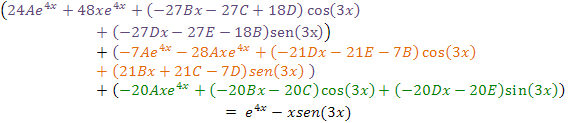
Agrupando términos semejantes:

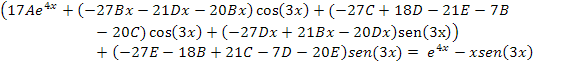
Paso 4: Establecer el sistema de Ecuaciones de los coeficientes
Ahora con la ecuación resultante del paso anterior:
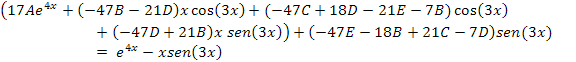
Establecemos la semejanza entre los términos de las ecuaciones, así:
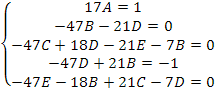
Al resolver el sistema de ecuaciones se tiene que:

Paso 5: Solución General
Con la solución complementaria y la solución particular tendremos como solución general de la Ecuación diferencial: