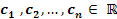Soluciones generales para ecuaciones diferenciales

1. Conjunto fundamental de Soluciones

Dada la ecuación diferencial lineal de orden n, y dadas las soluciones y₁, y₂, …, y_n soluciones linealmente independientes en un intervalo I, entonces el conjunto de n soluciones se denomina el conjunto fundamental de soluciones de la ecuación diferencial.

Veamos que el conjunto de funciones y¹ = e^x, y₂ = e^-x se constituye en el conjunto fundamental de soluciones para la ecuación y'' - y = 0. Para ello comprobemos las condiciones dadas por la definición.

1. La ecuación diferencial y'' - y = 0 es una ecuación diferencial de orden 2, por tanto el conjunto fundamental debe tener 2 soluciones elementales, en este caso:

   

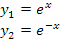
2. Revisemos que las soluciones son linealmente independientes para eso utilicemos un determinante definido, así:

   

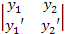
   En este caso, tenemos:

   

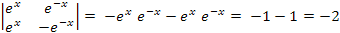
Ahora sabemos que si determinante es cero las soluciones son linealmente dependientes, por tanto en este caso -2 ≠ 0. Luego que las soluciones sean linealmente independientes.

En consecuencia, que el conjunto definido por { e^x, e^-x } se constituye en el conjunto fundamental de soluciones de la ecuación diferencial y'' -y = 0

Es importante formalizar la estrategia utilizada para revisar la independencia lineal, para ello, definimos el determinante Wronskiano con las soluciones de la ecuación diferencial así:

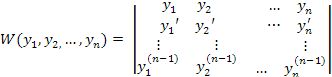
Diremos que el conjunto de soluciones es linealmente independiente si y sólo sí w ≠ 0

2. Solución general de una ecuación diferencial Homogénea

Para la ecuación diferencial lineal homogénea de grado (n) de la forma

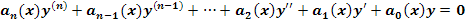
donde el conjunto fundamental de soluciones esta dado por: {y₁, y₂, y₃, …, y_n } en el intervalo I, entonces se tiene que la solución general esta dada por:

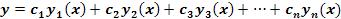
Ahora para una ecuación diferencial de No homogénea de la forma:

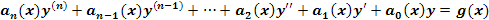
La solución general de la ecuación diferencial lineal de orden (n) esta dada por la suma de dos tipos de soluciones, denominadas así:

1. Solución complementaria: corresponde a la solución asociada a la ecuación diferencial lineal homogénea de orden (n) cuya notación es y_c
2. Solución particular asociada a la expresión g(x) cuya notación es y_p

3. Solución general de una ecuación diferencial No Homogénea

Para la ecuación diferencial lineal homogénea de grado (n) de la forma

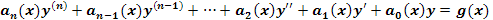
donde el conjunto fundamental de soluciones esta dado por: {y₁, y₂, y₃, …, y_n } en el intervalo I, entonces se tiene que la solución general esta dada por:

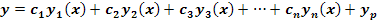
donde