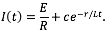Circuitos eléctricos simples
A partir de la ley de Ohm
E = IR
donde E es el voltaje, I es la intensisdad de corriente y R es la resistencia, y de la ley de Kirchhoff que afirma que la suma de las corrientes en un circuito cerrado es cero, entonces podemos análizar la razón de cambio de potencial en un circuito simple como el siguiente
Figura 1. Circuito
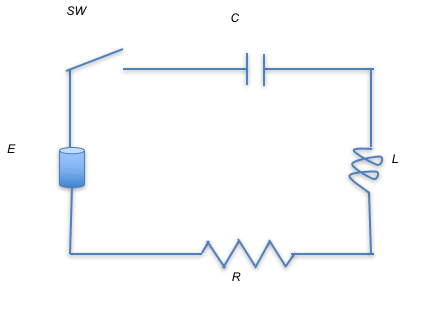
donde todos sus componentes están conectados en serie y contamos con un resistor con resistencia R, un inductor con una inductancia L, un capacitor con una capacitancia C y una batería que suministra un voltaje E.
El objetivo es observar como decae el voltaje a partir de que sale de la batería y recorre el circuito. Para ello y siguiendo las leyes físicas, tenemos que:
- Al cerrar el switch, la batería genera un flujo de corriente I(t) en el circuito y una carga Q(t) en el capacitor, las cuales están relacionadas por
- El capacitor almacena la carga Q(t) y esta se resiste a la entrada de carga extra y la caida de voltaje es proporcional a la carga existente, tal relación se da por
- El inductor pone una resistencia a los cambios de corriente y produce una caída de voltaje dada por
- La resistencia se opone al paso de corriente y produce una caída de voltaje dada por
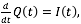
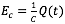

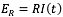
Así, se tiene que E-Ec-EL-ER=0, que puede escribirse como
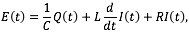
o
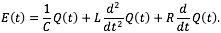
con variable dependiente Q(t), o
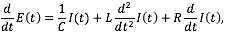
con variable dependiente I(t).
Tales ecuaciones son lineales de segundo orden, y su solución será vista en la siguiente unidad. Sin embargo, si en el circuito no hay capacitor y el voltaje es constante, entonces tenemos por ejemplo la ecuación de primer orden lineal
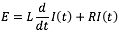
cuya solución es