Teorema de existencia de la solución única
Dada la ecuación diferencial:
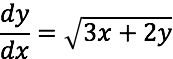
Determinemos la región del plano xy para la cual dicha ecuación tiene una única solución que satisface la condición (x0,y0). Para ello, analizamos las dos condiciones que propone el teorema:
-
g(x,y) es una función real y continua en todos los puntos de una región R
Veamos que 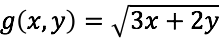
es una función definida y continua para: 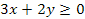
Esto es:
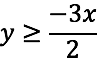
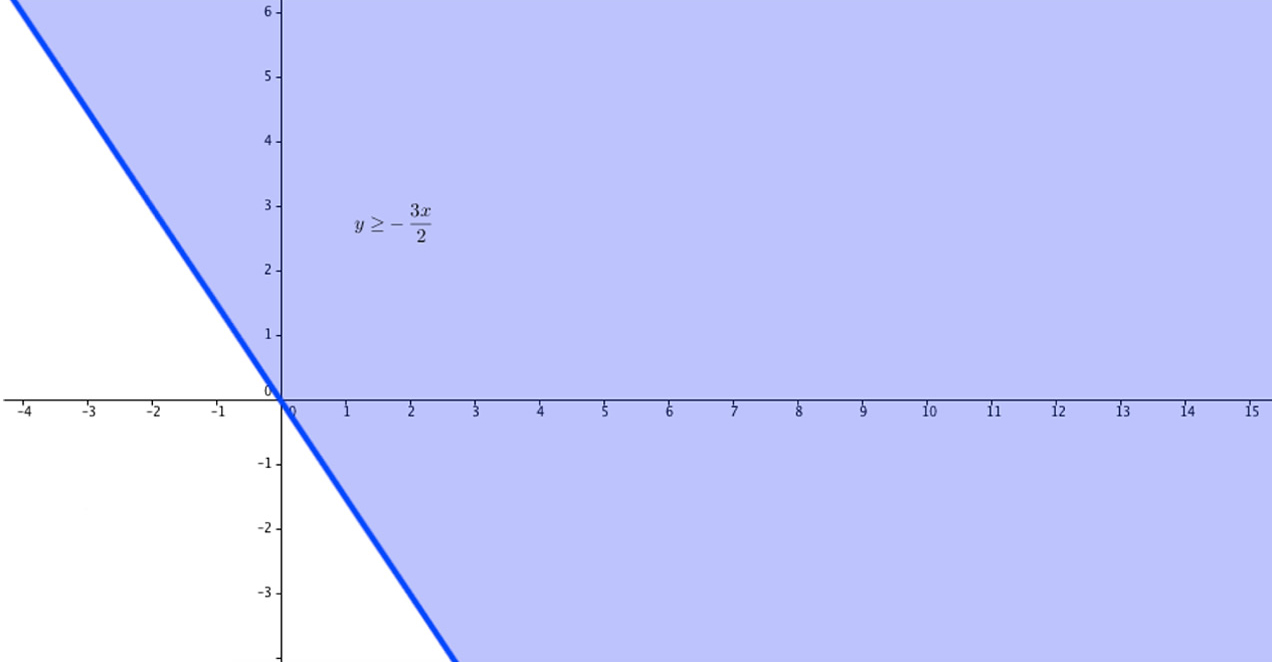
La región del plano que se define bajo esta condición es:
Figura 1. Región del plano para las soluciones particulares.
-
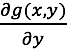
es una función real y continua en la región R 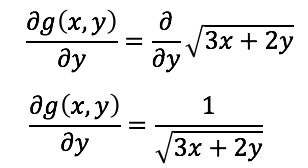
Y el análisis de la derivada nos define la siguiente región:
Figura 2. Región del plano para las soluciones particulares.
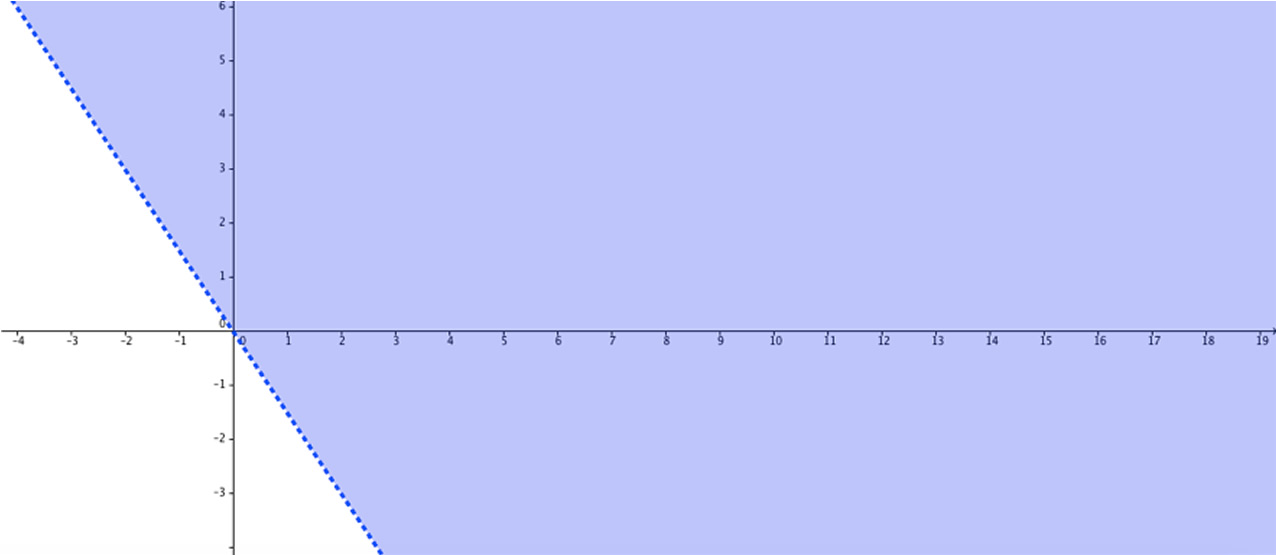
Esto significa que para cualquier punto de la región descrita en la anterior gráfica la ecuación diferencial tiene una única solución particular.
O de forma analítica la región es:
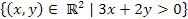
Ahora veamos lo que sucede para la siguiente condición:
