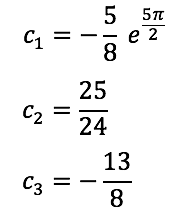Ejemplo como solución particular dadas las condiciones iniciales

Dada la ecuación diferencial

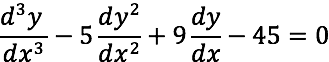
Sujeta a las siguientes condiciones:

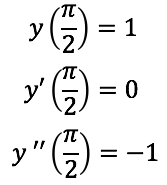
Se sabe que la familia triparamétrica de la forma y = c₁e^5x + c₂cos(3x) + c₃sen(3x), es solución de la ecuación, calculemos c₁,c₂,c₃ para las condiciones dadas. Es importante mencionar que si la función no es solución de la ecuación diferencial no es posible calcular las constantes por las condiciones iniciales.

Para esto iniciemos con el cálculo de la primera y la segunda derivada.

y = c₁e^5x + c₂cos(3x) + c₃sen(3x)

y' = 5c₁e^5x + 3c₂sen(3x) + 3c₃cos(3x)

y'' = 25c₁e^5x + 9c₂cos(3x) + 9c₃sen(3x)

Ahora con las condiciones iniciales sustituyamos en ellas:

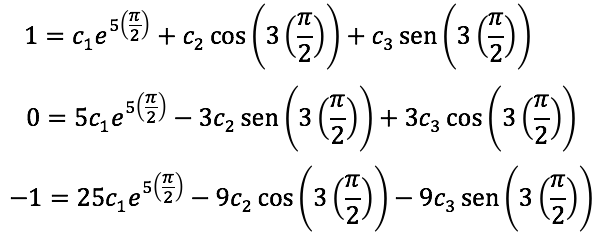
Al reducir la expresión tenemos:

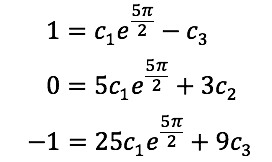
Y solucionando el sistema tenemos: