Solución de una Ecuación Diferencial

Para la ecuación diferencial:

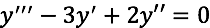
Una solución esta dada por:

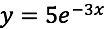
Veamos:

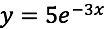
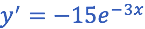
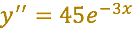
Ahora sustituyamos en la ecuación diferencial propuesta:

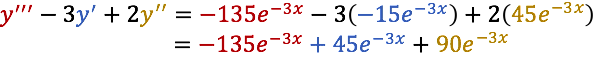
Observemos que la función y sus derivadas satisfacen la ecuación diferencial para todo x ϵ ℝ . Pero si pensamos en la siguiente solución:

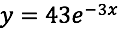
Volvemos a tener que:

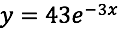
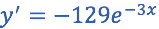
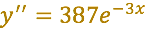
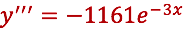
Ahora sustituyamos en la ecuación diferencial propuesta:

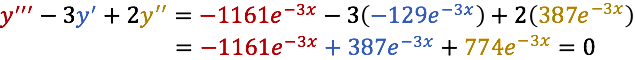
Observemos que la función y sus derivadas satisfacen la ecuación diferencial para todo x ϵ ℝ. De hecho cualquier función de la forma: y = Ae^-3x satisface la ecuación diferencial, para cualquier A ϵ ℝ.

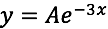
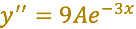
Ahora sustituyamos en la ecuación diferencial propuesta:

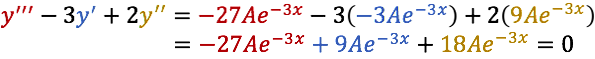
Por último, consideremos la siguiente expresión:

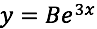
Donde B es cualquier constante. Comprobemos ahora si está función también es solución de la ecuación diferencial propuesta:

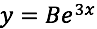
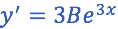
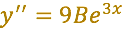
Sustituyendo tendremos:

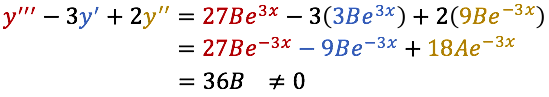
Luego que la función

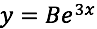
No sea solución de la ecuación diferencial

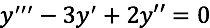
Este hecho es análogo para TODAS las ecuaciones diferenciales y se llama la Familia de Soluciones de la ecuación diferencial.