

Un contador es un circuito secuencial cuya función es seguir una cuenta o conjunto predeterminado de estados como consecuencia de la aplicación de un tren de pulsos (señal de reloj) en una de sus entradas. Los contadores son construidos con base en flip-flops, sincronizados por flanco, y compuertas lógicas que se encargan de realizar la conexión entre los flip-flops.
Las puertas lógicas que se usan en un contador se conectan de forma que fuercen a los flip-flops a seguir la secuencia prescrita de estados, predeterminada por el diseñador o el usuario, según el caso.
Es la principal aplicación de los flip flop y a su vez es uno de los elementos más usados en el mundo real, donde se cuenta todo, debido a la necesidad de medir. Estos dispositivos permiten contar en forma automática y segura con errores mínimos e incluso nulos.
Existen tres versiones: asincrónicos, sincrónicos y especiales.
Son aquellos en los que el cambio de estado del primer ciclo (flip flop) controla el segundo y así sucesivamente. Es decir, solo requieren la conexión del pulso de reloj en el primer flip flop para funcionar y no requieren estar sincronizados en el tiempo para su funcionamiento. Son muy limitados en velocidad de respuesta, debido a la propagación de señal y pueden ocurrir demoras importantes según la aplicación.
Son aquellos que requieren de un reloj sincronizado en el tiempo para que su funcionamiento y operación se lleve a cabo. El pulso de reloj se conecta en paralelo a todos los flip flops y su circuito requiere un poco más de complejidad dependiendo de la aplicación y la secuencia de cuenta. Su velocidad de respuesta es alta, pero consumen mucha más energía que los asincrónicos.
Dentro de estos tenemos dos tipos específicos de contadores: binarios y no binarios o especiales:
Estos contadores se implementan como autómatas debido a que no poseen entradas diferentes a la señal de reloj, el cual controla por flanco la cuenta establecida; además que su salida es el estado interno de cada flip flop. Para su diseño se usan las ecuaciones de estado de los flip flop.
Diseñar un contador binario de módulo 8, es decir de tres bits.
Solución
El contador seguirá la secuencia 0, 1, 2, 3, 4, 5, 6, 7, 0, 1, 2, …….., es decir es un contador cíclico o de ciclo cerrado. Ahora procedemos a obtener la tabla de estado del contador usando para ello los estados de los flip flop.
| Estado actual (Qn) | Estado siguiente (Qn+1) | ||||
| Q2 | Q1 | Q0 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 |
Como se va a diseñar con flip flop JK, se usa la tabla de transiciones de los Flip flop para este diseño.
| Estado actual (Qn) | Estado siguiente (Qn+1) | Transición de flip flop | ||||||
| Q2 | Q1 | Q0 | Q2 | Q1 | Q0 | J2 K2 | J1 K1 | J0 K0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 X | 0 X | 1 X |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 X | 1 X | X 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 X | X 1 | X 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 0 X | X 0 | 1 X |
| 1 | 0 | 0 | 1 | 0 | 1 | X 0 | X 0 | 1 X |
| 1 | 0 | 1 | 1 | 1 | 0 | X 1 | X 1 | X 1 |
| 1 | 1 | 0 | 1 | 1 | 1 | X 0 | 1 X | X 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | X 0 | 0 X | 1 X |
De acuerdo con la tabla anterior, se procede a encontrar las expresiones algebraicas para las entradas J y K de los Flip flop según el estado actual. Para ello se minimizan las funciones de cada Flip flop usando mapas de Karnaugh.
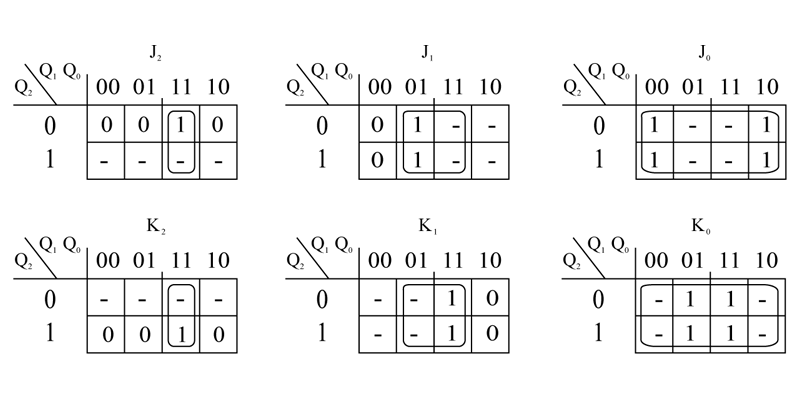
La reducción da como resultado:
Jo = Ko = 1
J1 = K1 = Qo
J2 = K2 = Q1Qo
El siguiente es el circuito implementado el contador:

En este contador al realizar el diagrama de tiempos para las señales que intervienen en el proceso se obtiene la gráfica vv.

También se pueden implementar con cualquier tipo de flip flop, ya sea RS, T, D, o como en este caso con JK.
Estos contadores realizan secuencias diversas. Algunas de ellas, con patrones muy específicos acorde a la aplicación requerida para el circuito y se implementan con cualquier tipo de Flip flop, ya sea RS, D, T o JK.
Diseñar un contador que realice la secuencia 0, 7, 5, 3, 4, 2 en forma cíclica.
Para este caso se procede primero a elegir los Flip flop; en este caso se emplearán los de tipo T. Posteriormente, se realiza la tabla de estados del contador.
| Estado actual (Qn) | Estado siguiente (Qn+1) | ||||
| Q2 | Q1 | Q0 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
Ahora se procede a realizar la tabla de transición de estados para el flip flop T.
| Estado actual (Qn) | Estado siguiente (Qn+1) | Transición de flip flop | ||||||
| Q2 | Q1 | Q0 | Q2 | Q1 | Q0 | T2 | T1 | T0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
Utilizando el mapa de Karnaugh para minimizar las funciones de la tabla de transiciones del flip fop, se obtiene:

De donde sale como función para las T respectivas:

Para la implementación circuital queda como esquemático del contador del ejemplo el siguiente gráfico.

Cuando se aplica la señal de reloj y se analiza la respuesta en el diagrama de tiempos del contador se obtiene como salida, el diagrama de la grafica tt.

Es de anotar que existen comercialmente contadores de carga paralelo, contadores ascendentes y/o descendentes que usan un bit de control o una entrada de control, la cual actúa en un sentido con 0 y con 1 en otro sentido.