En este caso, con todos los términos de la tabla de verdad, se saca la función homogénea, se reduce por algebra de Boole o por Mapas de Karnaugh y una vez reducida se implementa esta función.
Implementar la función que corresponde a la tabla de verdad.
| A | B | C | D | X |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
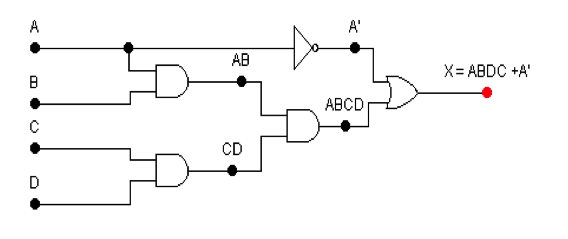
Se deduce que la salida vale 1 para 0, 1, 2, 3, 4, 5, 6, 7 y 15, de ahí que al hacer uso del Mapa de Karnaugh de cuatro variables queda:
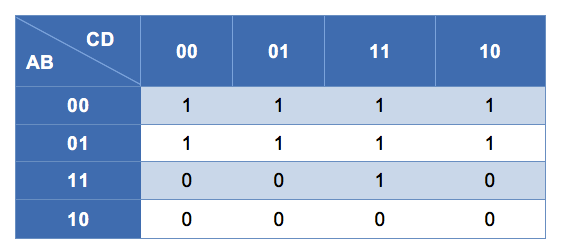
Al reducir la función queda: X=ABCD+A’ con la implementación de AND, OR e Inversores.