

Son una poderosa herramienta de reducción de funciones lógicas con la que se puede reducir fácilmente cualquier función de variables con la ayuda de un computador y hasta una función de cinco variables en forma manual.
En los mapas es muy importante mantener la relación de pesos, de tal forma que los pesos más significativos van en las filas y los menos significativos van en las columnas, conformando una matriz de tamaño dependiente del número de variables, donde el mínimo número es dos.
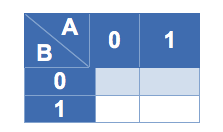
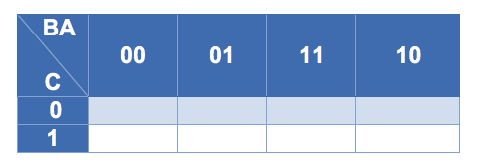
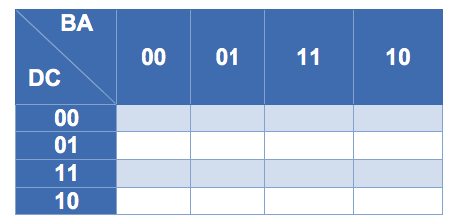
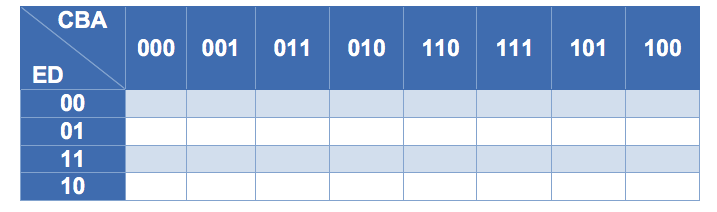
Es importante notar que el orden de los valores en cada casilla están dispuestos de tal forma que garantizan la adyacencia entre casillas por todo lado en el mapa, lo cual es requisito fundamental para poder aplicar reducción utilizando el método de mapas de Karnaugh.
Cada celda corresponde a un término, en suma de productos se agrupan los unos (1) adyacentes, por filas y columnas; no hay adyacencia en las diagonales, para agrupar se deben realizar grupos de 2n celdas, es decir, 1, 2, 4, 8, etc.
Cuando se agrupa, se eliminan n celdas de la agrupación, es decir, si agrupo 4 celdas (22), entonces se eliminan dos variables (n), permaneciendo las variables que no cambian a través de las celdas. Se recomienda que al agrupar debe haber por lo menos un uno (1) que no se había agrupado antes.
Reducir las siguientes funciones usando mapas de Karnaugh:
Solución:
Es un mapa de cuatro variables (DCBA), entonces dibujamos este mapa así, y colocamos los unos según corresponda, agrupando nos queda:
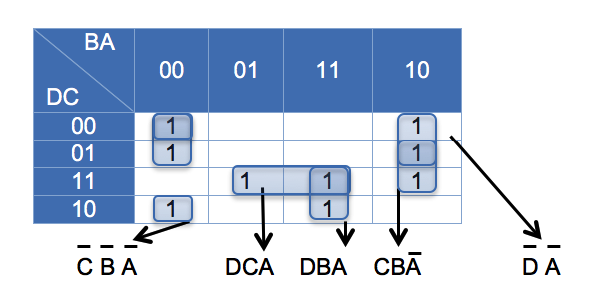
Como puede verse resultan cinco agrupaciones diferentes, para poder agrupar todos los unos necesarios.
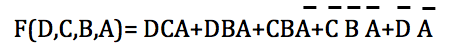
Como se puede ver la función se redujo considerablemente.
Vemos que es un mapa de dos variables, luego lo dibujamos y ubicamos los unos en su respectiva posición, para luego reducir las adyacencias.
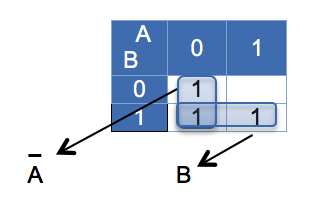
Es posible determinar que se reduce a dos expresiones simples, de tal manera que la función reducida queda:
