

El proceso de construcción de funciones y expresiones lógicas en sistemas digitales usa dos procesos principales: la suma de productos y el producto de sumas; ambas en forma canónica.
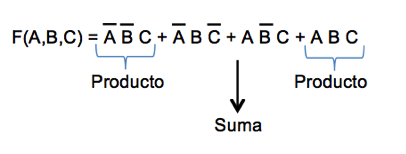
Es la representación usando suma de productos de forma canónica, cuyo símbolo normalmente es la sumatoria, donde los términos mínimos o min términos deben ser igual a uno. Es decir, uno es el valor directo o no negado de los términos.
Sea F (A,B,C) = ∑ (1,2,5,7), significa que para los valores (binario) 1, 2, 5, 7 la función f tendrá un valor de uno en esos valores.
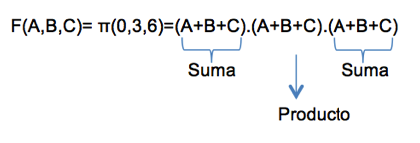
Es la representación usando productos de sumas de forma canónica, cuyo símbolo normalmente es la productoria, donde los términos máximos o máx. Términos deben ser igual a cero. Es decir, el cero es el valor directo o no negado de los términos.
Sea F (A,B,C) = π (0,3,6), significa que para los valores (binarios) 0, 3 y 6 F toma un valor de cero.
Es una forma de representar las posibles combinaciones binarias que se pueden presentar con las variables de entrada y acorde a ellas representar la función (es) de salida.
Representar la función f(A,B,C)=∑(0,2,4,6,7) en una tabla de verdad.
Solución:Se puede ver que son tres variables, por lo tanto 23 = 8; es decir, se tienen ocho combinaciones posibles.
| A | B | C | F (A, B, C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Como vemos en la tabla la función toma el valor de uno (1) para los datos indicados.