Nivel Discreto

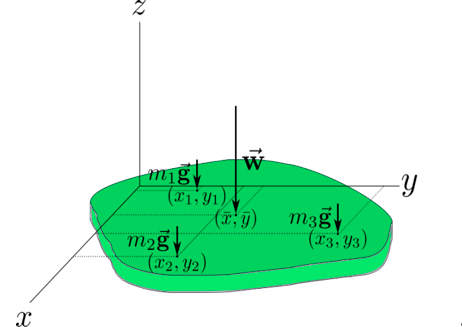
Inicialmente, si se considera un cuerpo rígido compuesto de una distribución de partículas en un campo gravitacional uniforme, entonces sobre cada una de ellas actúa la fuerza de gravedad con la misma intensidad. De tal manera que existen n-vectores de peso w_i = m_ig con i= 1,2, ... ,n (ver figura a).

La fuerza resultante w corresponde en este caso discreto a la suma de los n-ésimos vectores de peso de la distribución. Se define la suma sobre las magnitudes de los pesos, de esta manera:

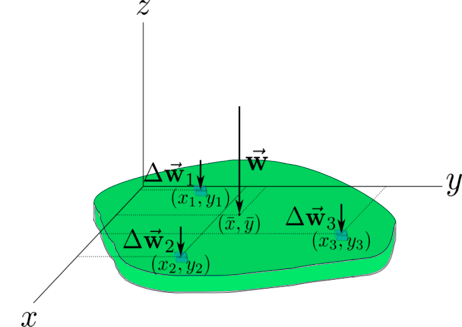
En el caso de considerar una distribución con n elementos de peso ∆w (ver figura b), la fuerza resultante w se ubica en el centro de gravedad CG con coordenadas x→ e y→ y constituye dicho vector la suma de todos los diferenciales de peso ∆w_i. Se define la suma sobre las magnitudes de los pesos, así:

Pero, ¿cómo se determina el centro de gravedad? Para dar respuesta a este interrogante se consideran los n elementos de peso ∆w. A partir de cada se define su momento de fuerza τ que es igual al producto de ∆w por su brazo de momento. Por lo tanto, se establece que la suma de todos los momentos de fuerza generados por los pesos con relación a los ejes e son:

Determinar las coordenadas x→ e y→ del punto CG, en donde se ubica w, se hace a partir de la suma de los momentos de fuerza definidos anteriormente tanto para a la coordenada x como para la de y, tal que:

Ahora bien, considerando una distribución de masa continua y no discreta en el cuerpo rígido, se calcula el límite para la sumatoria de tal forma que:

De manera similar se calcula el límite en la sumatorias de los momentos de fuerza x→w y y→w para determinar las coordenadas x→ e y→w del punto CG, por lo cual:

Nivel Continuo

Las expresiones que determinan la fuerza resultante w y las coordenadas x→ e y→ para encontrar el centro de gravedad de un objeto determinado son: