Momento de inercia de masas

Considere una masa m que puede girar alrededor de un eje A como lo muestra la siguiente figura. Si de esa masa se toma un pequeño elemento diferencial dm a una distancia r perpendicular al eje A, la medida de la inercia de éste pequeño elemento es proporcional al producto del cuadrado de su distancia al eje de rotación r² y al diferencial de masa dm. Es decir, que el producto r²dm es el llamado momento de inercia de la masa dm

Ahora bien, para saber cuál es el momento de inercia de la masa completa m, lo que se debe hacer es sumar todos los momentos de inercia que aporta cada elemento diferencial, de tal forma que al incrementar el número de elementos diferenciales al límite, se obtiene una integral dada por la expresión:

Si se supone que se concentra toda la masa del cuerpo en un punto entonces, el momento de inercia estará dado por:

Donde k es el radio de giro del o la distancia a la que se debe concentrar la masa del cuerpo y tiene unidades de kgm²

El momento de inercia del cuerpo se puede expresar en términos de las coordenadas x, y, z del elemento de masa dm, ya que como se muestra en la siguiente figura, r²=z²+x²

Por tanto:

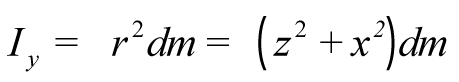y reproduciendo el mismo razonamiento para los demás ejes coordenados, se encuentra que:

Para ésta situación también es posible aplicar el teorema de Steiner o de los ejes paralelos, si se desea hallar el momento de inercia del cuerpo respecto otro sistemas de coordenadas x, y, z, paralelo al sistemas de coordenadas x', y', z' que se encuentra ubicado en el centro de gravedad (G) del cuerpo.

La relación entre las coordenadas del sistema no primado x, y, z y el sistema primado x', y', z' del elemento de masa dm está dado por:

Donde las cantidades x→, y→, z→ representan las coordenadas del origen para el sistema primado, que son las mismas coordenadas del centro de gravedad del cuerpo.

Con las relaciones anteriores es posible aplicar el teorema de los ejes paralelos y se encuentra respecto a cada eje coordenado que:

Generalizando, el momento de inercia de un cuerpo respecto a un eje paralelo a otro que pase por su centro de gravedad está dado por la relación:

Donde I' representa el momento de inercia del cuerpo respecto a un eje que pasa por su centro de gravedad y d² representa el cuadrado de la distancia entre los dos ejes (ver figura)

La relación entre los radios de giro correspondientes a los ejes es:

donde, la k barrada representa el radio de giro respecto al eje que pasa por el centro de gravedad del cuerpo.