Momentos principales de inercia

En ocasiones es necesario encontrar los momentos de inercia y el producto de inercia respecto a un sistema de coordenadas rotado con respecto a otro de referencia, tal y como se muestra en la siguiente figura:

De acuerdo con los datos dados en la gráfica, se pueden extraer relaciones entre los dos sistemas mediante el uso de la geometría básica, donde se pueden encontrar las siguientes equivalencias:

y remplazando estas expresiones en las integrales de los momentos de inercia y del producto de inercia, con respecto a los ejes x' , y' y simplificando usando funciones trigonométricas, se encuentra que los momentos y producto de inercia respecto a los ejes primados son:

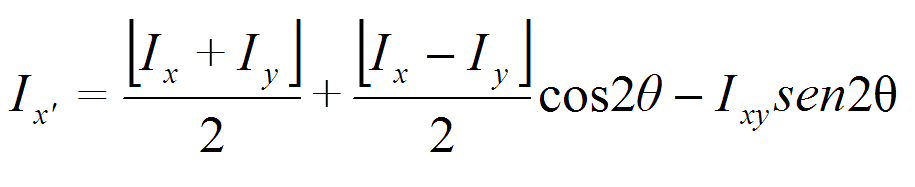
Ahora bien, como se puede ver en las expresiones anteriores, todas dependen del ángulo de inclinación de los ejes primados, lo que permite encontrar momentos de inercia máximos y mínimos para el área A, respecto a un sistema particular de ejes llamados ejes principales.

El ángulo que determina la orientación de los ejes principales θ_m, está dado por:

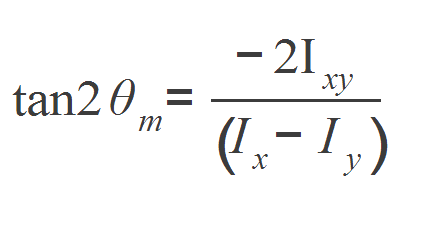
Esto se obtiene derivando respecto a θ, la primera ecuación del momento de inercia respecto a x' e igualando a cero el resultado.

El ángulo θ_m, medido a partir del eje x, de referencia de la figura, indica la posición del eje x principal y al sumarle 90 grados, a éste mismo ángulo, se encuentra el eje y principal de la figura.

Con la anterior expresión es posible encontrar los momentos máximo y mínimo del área A dados por:

Donde escogiendo el signo positivo, se encuentra el momento de inercia máximo y escogiendo el signo negativo, se encuentra el momento de inercia mínimo del área A.

Con las expresiones anteriores también es posible mostrar que el producto de inercia I_x'y' es cero con respecto a los ejes principales, lo cual quiere decir que todo eje principal representa un eje de simetría del área A.