Teorema de los ejes paralelos

Considere la siguiente figura:

Sea (y), la distancia entre el eje x' y el elemento de área dA, entonces, el momento de inercia del área A respecto del eje x, dadas las definiciones anteriores es:

Dada (y') como la distancia entre el eje x centroidal y el elemento de área dA, se encuentra que y=y'+d, donde (d) es la distancia entre los ejes x y x', de tal forma que:

Donde la primera integral da cuenta del momento de inercia del área A respecto al eje x, la segunda integral es cero ya que representa el primer momento del área A respecto a el eje x, que pasa por el centroide, y la tercera integral es igual a área A multiplicada por el cuadrado de la distancia (d) entre los dos ejes.

Por tanto, se encuentra que el momento de inercia respecto al eje (x') es:

Extendiendo el mismo razonamiento para los eje y' y y, se encuentra que el momento de inercia respecto al eje y':

y respecto al eje polar, el momento de inercia respecto a un eje perpendicular al plano, x'y' que pasa a través del polo O es:

Con lo anterior, se puede decir que el momento de inercia de un área A respecto a un eje, es igual al momento de inercia del área respecto a un eje que pasa por el centroide de dicha área, más el producto del cuadrado de la distancia entre los dos ejes y el área.

Es importante tener en cuenta que el término Ad² se debe sumar cuando se pasa de un eje centroidal a uno paralelo y se debe restar, cuando se pasa de un eje paralelo a uno centroidal. De tal forma que el momento de inercia, respecto a un eje paralelo, sea mayor que al centroidal.

Ahora bien, el mismo teorema se puede expresar en términos del radio de giro, usando la definición del momento de inercia en términos del mismo I=k²A, de tal forma que para el eje x':

para el eje y' :

Y para el eje polar:

Ejemplo

Por medio del teorema de Steiner, se demuestra que los momentos de inercia respecto al eje x'y' del rectángulo en la siguiente figura son:

Dado que el área del rectángulo es A=bh y que el momento de inercia respecto al eje x para un rectángulo está definido como 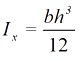para el eje y como 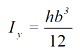entonces, aplicando el teorema de Steiner para eje x:

y para el eje y: